Bài 10 trang 106 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đặc biệt là các tính chất của hình thang cân để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 106 Vở thực hành Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
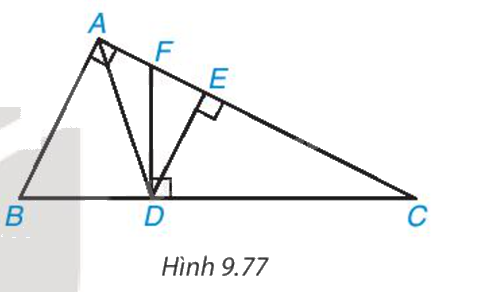
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:
Đề bài
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:
a) \(\frac{B\text{D}}{BC}=\frac{AB}{AB+AC}\), từ đó suy ra \(A\text{E}=\frac{AB.AC}{AB+AC}\);
b) ΔDFC ∽ ΔABC;
c) DF = DB
Phương pháp giải - Xem chi tiết
Sử dụng các tam giác đồng dạng để chứng minh.
Lời giải chi tiết
a) Kẻ đường thẳng qua D vuông góc và cắt AB tại K. Khi đó DK = AE.
Vì DE // AB, DK // AC nên $\Delta BDK\backsim \Delta BCA$ và $\Delta CDE\backsim \Delta CBA$.
Suy ra $\frac{BD}{BC}=\frac{DK}{CA}=\frac{DE}{CA}=\frac{DE}{BA}.\frac{BA}{CA}=\frac{DC}{BC}.\frac{AB}{AC}$.
Do vậy $BD=\frac{DC.AB}{AC}$ , hay $\frac{DC}{BD}=\frac{AB}{AC}$ (*)
Từ (*) suy ra $\frac{BC}{BD}=1+\frac{DC}{BD}=1+\frac{AC}{AB}=\frac{AB+AC}{AB}$, do đó $\frac{BD}{BC}=\frac{AB}{AB+AC}$.
Theo định lí Thalès, ta có: $\frac{AE}{AC}=\frac{BD}{BC}=\frac{AB}{AB+AC}$. Suy ra AE = \(\frac{AB.AC}{AB+AC}\).
b) Hai tam giác vuông DFC (vuông tại D) và ABC (vuông tại A) có góc nhọn C chung nên $\Delta DFC\backsim \Delta ABC$ suy ra $\frac{DF}{AB}=\frac{DC}{AC}=\frac{DC}{DB}.\frac{DB}{AC}=\frac{AC}{AB}.\frac{DB}{AC}=\frac{DB}{AB}$.
Do đó DF = DB.
Bài 10 trang 106 Vở thực hành Toán 8 tập 2 yêu cầu chúng ta giải một bài toán liên quan đến hình thang cân. Cụ thể, bài toán thường cho một hình thang cân với các thông tin về độ dài các cạnh, đường cao, hoặc các góc. Nhiệm vụ của chúng ta là tính toán các yếu tố còn lại của hình thang cân đó, ví dụ như độ dài đường trung bình, diện tích, hoặc các góc chưa biết.
Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài toán. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một số bước giải chung:
Giả sử bài toán yêu cầu tính độ dài đường trung bình của hình thang cân ABCD, biết AB = 10cm, CD = 16cm.
Lời giải:
Áp dụng công thức tính đường trung bình của hình thang, ta có:
m = (AB + CD) / 2 = (10 + 16) / 2 = 13cm
Vậy, độ dài đường trung bình của hình thang cân ABCD là 13cm.
Để củng cố kiến thức về hình thang cân và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập sau:
Bài 10 trang 106 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp các em học sinh hiểu sâu hơn về hình thang cân và các tính chất của nó. Bằng cách nắm vững kiến thức và áp dụng các phương pháp giải phù hợp, các em có thể tự tin giải quyết các bài tập tương tự một cách hiệu quả.
| Công thức | Mô tả |
|---|---|
| S = (a + b) * h / 2 | Diện tích hình thang |
| m = (a + b) / 2 | Đường trung bình hình thang |
| a2 + b2 = c2 | Định lý Pitago |