Bài 13 trang 107 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đặc biệt là các tính chất của hình thang cân để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 13 trang 107 VTH Toán 8 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
Cho tam giác ABC vuông tại A có AB = 16 cm, AC = 12 cm. Kẻ đường phân giác BD (D thuộc AC). Tính độ dài các đoạn thẳng CD và AD.
Đề bài
Cho tam giác ABC vuông tại A có AB = 16 cm, AC = 12 cm. Kẻ đường phân giác BD (D thuộc AC). Tính độ dài các đoạn thẳng CD và AD.
Phương pháp giải - Xem chi tiết
Chứng minh ΔOAB ∽ ΔOCD suy ra các tỉ số đồng dạng và khoảng cách từ căn hộ nhà Lan đến tòa nhà đối diện là 29m.
Lời giải chi tiết
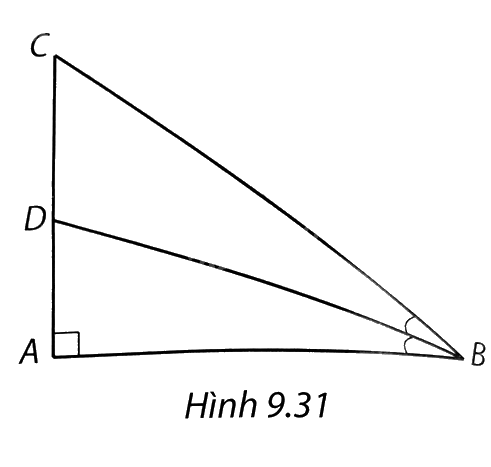
(H.9.31). Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta được:
BC2 = AB2 + AC2 = 400. Suy ra BC = 20cm.
Do BD là phân giác góc ABC nên:
$\frac{AD}{AB}=\frac{CD}{BC}=\frac{AD+CD}{AB+BC}=\frac{12}{36}=\frac{1}{3}$.
Suy ra $AD=\frac{AB}{3}=\frac{16}{3}cm,CD=\frac{BC}{3}=\frac{20}{3}cm.$.
Bài 13 trang 107 Vở thực hành Toán 8 tập 2 yêu cầu chúng ta giải một bài toán liên quan đến hình thang cân. Cụ thể, bài toán thường cho một hình thang cân với các thông tin về độ dài các cạnh, góc hoặc đường chéo, và yêu cầu tính toán các yếu tố còn lại như chiều cao, diện tích, hoặc chứng minh một đẳng thức nào đó.
Để giải bài toán hình thang cân một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, hình vẽ minh họa và giải thích rõ ràng. Ví dụ, nếu bài toán yêu cầu tính chiều cao của hình thang cân, lời giải sẽ trình bày các bước sử dụng định lý Pitago hoặc các tính chất của tam giác vuông để tính toán chiều cao đó.)
Giả sử bài toán cho hình thang cân ABCD có AB = 5cm, CD = 10cm, AD = BC = 6cm. Hãy tính chiều cao của hình thang.
Giải:
Vậy chiều cao của hình thang cân ABCD là khoảng 5.45cm.
Để nắm vững kiến thức về hình thang cân và rèn luyện kỹ năng giải toán, các em có thể tham khảo thêm các bài tập sau:
Bài 13 trang 107 Vở thực hành Toán 8 tập 2 là một bài tập điển hình về hình thang cân. Việc nắm vững các kiến thức và phương pháp giải bài toán này sẽ giúp các em học sinh tự tin hơn trong việc giải quyết các bài toán hình học khác. Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ hiểu rõ hơn về bài toán này và đạt kết quả tốt trong học tập.
| Công thức | Mô tả |
|---|---|
| S = (a + b)h/2 | Diện tích hình thang |
| m = (a + b)/2 | Đường trung bình của hình thang |
| a2 + b2 = c2 | Định lý Pitago |