Bài 8 trang 105 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các phép biến đổi đại số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 105 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:
Đề bài
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:
a) \(\frac{B\text{D}}{BC}=\frac{AB}{AB+AC}\), từ đó suy ra \(A\text{E}=\frac{AB.AC}{AB+AC}\)
b) ΔDFC ∽ ΔABC
c) DF=DB
Phương pháp giải - Xem chi tiết
Sử dụng các tam giác đồng dạng để chứng minh
Lời giải chi tiết
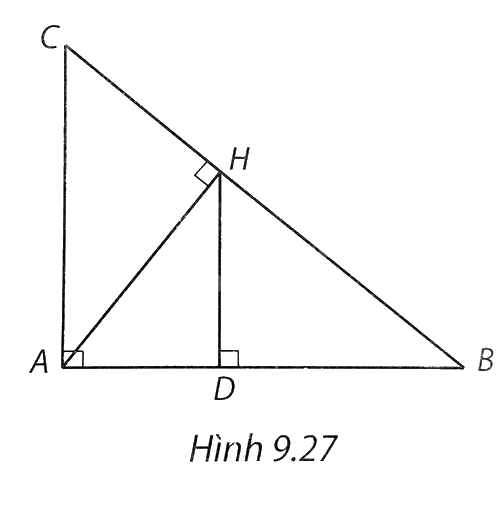
a) Hai tam giác vuông HDA (vuông tại D) và AHC (vuông tại H) có: $\widehat{DAH}={{90}^{0}}-\widehat{ACB}=\widehat{HCA}$.
Do đó $\Delta HDA\backsim \Delta AHC$ (cặp góc nhọn).
b) Áp dụng định lí Pythagore cho tam giác ABC vuông tại đỉnh A, ta có:
$B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}=41$, hay $BC=\sqrt{41}$ cm.
Mặt khác, trong tam giác vuông ABC với đường cao AH, ta có:
+) $AH.BC=2{{S}_{ABC}}=AB.AC$.
Do đó $AH=\frac{AB.AC}{BC}=\frac{20}{\sqrt{41}}$ (cm).
+) $A{{B}^{2}}=BH.BC$. Do đó $BH=\frac{A{{B}^{2}}}{BC}=\frac{25}{\sqrt{41}}$ (cm).
+) $A{{C}^{2}}=CH.BC$. Do đó $CH=\frac{A{{C}^{2}}}{BC}=\frac{16}{\sqrt{41}}$ (cm).
+ $HD=\frac{BH.AC}{BC}=\frac{\frac{25}{\sqrt{41}}.4}{\sqrt{41}}=\frac{100}{41}$ (cm).
Bài 8 trang 105 Vở thực hành Toán 8 tập 2 thuộc chương trình đại số, tập trung vào việc vận dụng các kiến thức về phân tích đa thức thành nhân tử, đặc biệt là sử dụng các phương pháp như đặt nhân tử chung, dùng hằng đẳng thức, và nhóm đa thức.
Bài tập yêu cầu học sinh phân tích các đa thức sau thành nhân tử:
Để giải bài này, ta đặt nhân tử chung là 3x:
3x2 - 6x = 3x(x - 2)
Đây là một hằng đẳng thức quen thuộc: (a - b)2 = a2 - 2ab + b2. Trong trường hợp này, a = x và b = 2:
x2 - 4x + 4 = (x - 2)2
Đây là tổng hai lập phương: a3 + b3 = (a + b)(a2 - ab + b2). Trong trường hợp này, a = x và b = 2:
x3 + 8 = (x + 2)(x2 - 2x + 4)
Đây là hiệu hai bình phương: a2 - b2 = (a + b)(a - b). Trong trường hợp này, a = x và b = 5:
x2 - 25 = (x + 5)(x - 5)
Đây là hiệu hai lập phương: a3 - b3 = (a - b)(a2 + ab + b2). Trong trường hợp này, a = x và b = 3:
x3 - 27 = (x - 3)(x2 + 3x + 9)
Đây là một hằng đẳng thức quen thuộc: (a + b)2 = a2 + 2ab + b2. Trong trường hợp này, a = x và b = 2:
x2 + 4x + 4 = (x + 2)2
Để phân tích đa thức thành nhân tử, cần nắm vững các phương pháp sau:
Phân tích đa thức thành nhân tử là một kỹ năng quan trọng trong Toán học, có nhiều ứng dụng trong việc:
Bài 8 trang 105 Vở thực hành Toán 8 tập 2 là một bài tập cơ bản nhưng quan trọng để củng cố kiến thức về phân tích đa thức thành nhân tử. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.