Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Giải bài 11 trang 101 Vở thực hành Toán 8. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài viết này sẽ trình bày đầy đủ các bước giải, phân tích và giải thích chi tiết để bạn có thể hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Bảng thống kê sau cho biết số lượng học sinh của các lớp khối 8 tham gia các câu lạc bộ Thể thao và Nghệ thuật của trường.
Đề bài
Bảng thống kê sau cho biết số lượng học sinh của các lớp khối 8 tham gia các câu lạc bộ Thể thao và Nghệ thuật của trường.
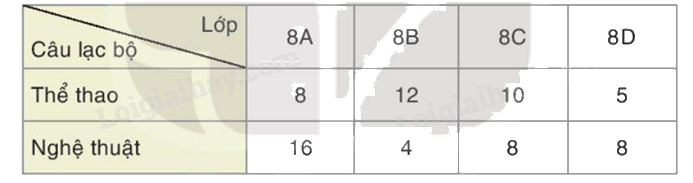
a) Lựa chọn và vẽ biểu đồ để so sánh số lượng học sinh tham gia hai câu lạc bộ này ở từng lớp.
b) Lựa chọn và vẽ biểu đồ biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này.
Phương pháp giải - Xem chi tiết
Dựa vào bảng thống kê và yêu cầu của đề bài để lựa chọn biểu đồ cho hợp lí
Lời giải chi tiết
a) Biểu đồ so sánh số học sinh tham gia hai câu lạc bộ ở từng lớp:
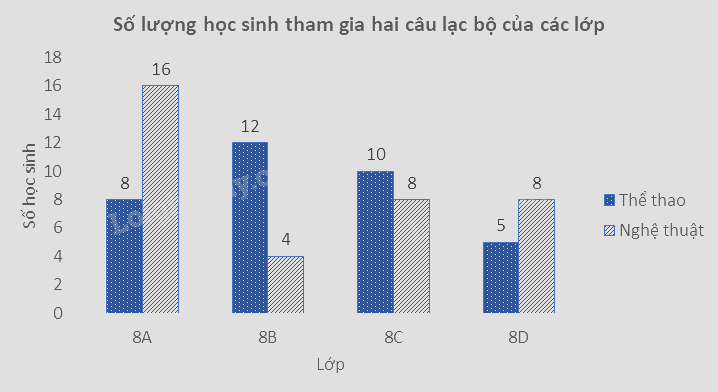
b) Để biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này ta nên dùng biểu đồ hình quạt tròn.
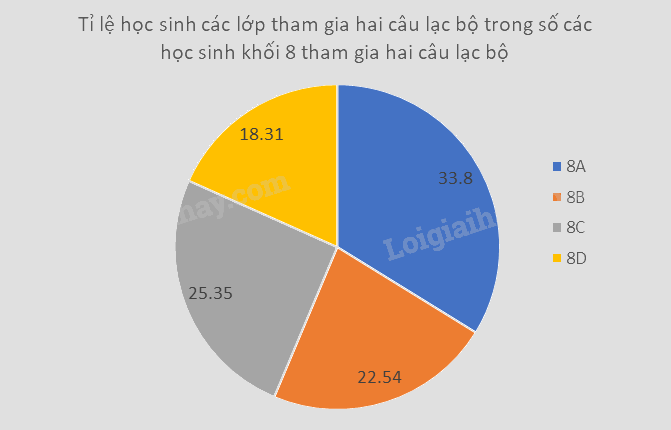
Bài 11 trang 101 Vở thực hành Toán 8 thường thuộc chương trình học về các kiến thức liên quan đến hình học, cụ thể là các dạng bài tập về tứ giác, hình thang, hoặc các tính chất của đường thẳng song song. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, định lý và tính chất cơ bản của các hình đã học.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp bạn tránh được những sai sót không đáng có và tìm ra phương pháp giải phù hợp nhất. Hãy chú ý đến các dữ kiện đã cho, các hình vẽ minh họa và các câu hỏi cụ thể mà đề bài đặt ra.
Dưới đây là lời giải chi tiết cho bài 11 trang 101 Vở thực hành Toán 8. (Lưu ý: Vì đề bài cụ thể không được cung cấp, phần này sẽ trình bày một ví dụ minh họa về cách giải một bài tập hình học thường gặp.)
Đề bài: Cho hình thang ABCD (AB // CD). Gọi M là trung điểm của AD, N là trung điểm của BC. Chứng minh rằng MN // AB // CD và MN = (AB + CD) / 2.
Lời giải:
Ngoài bài tập trên, còn rất nhiều dạng bài tập tương tự liên quan đến hình thang và các tính chất của đường thẳng song song. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách giáo khoa, sách bài tập và các nguồn tài liệu học tập khác. Hãy tìm kiếm các bài tập có độ khó tăng dần để thử thách bản thân và nâng cao khả năng giải quyết vấn đề.
Bài 11 trang 101 Vở thực hành Toán 8 là một bài tập quan trọng giúp bạn rèn luyện các kiến thức và kỹ năng về hình học. Hy vọng rằng với lời giải chi tiết và các phương pháp giải đã trình bày, bạn sẽ tự tin hơn khi đối mặt với các bài tập tương tự. Chúc bạn học tập tốt!