Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 74 Vở thực hành Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập môn Toán, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho tam giác ABC, trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E.
Đề bài
Cho tam giác ABC, trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E.
a) Chứng minh: DC // EM.
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất đường trung bình của tam giác.
Lời giải chi tiết
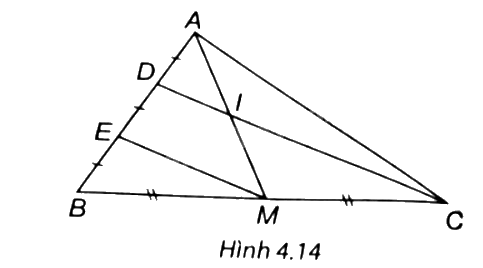
(H.4.14). a) ∆BDC có: E là trung điểm BD; M là trung điểm BC nên EM là đường trung bình của ∆BDC.
Suy ra DC // EM.
b) ∆AEM có: D là trung điểm AE, DI // EM (vì DC // EM).
Suy ra I là trung điểm AM.
Bài 3 trang 74 Vở thực hành Toán 8 thường thuộc các dạng bài tập về hình học, cụ thể là các bài toán liên quan đến tứ giác, hình thang, hoặc các tính chất của đường thẳng song song. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về các khái niệm hình học, các định lý và tính chất liên quan.
Thông thường, bài 3 trang 74 sẽ bao gồm một hoặc nhiều câu hỏi yêu cầu học sinh:
Để giải bài 3 trang 74 Vở thực hành Toán 8, học sinh có thể áp dụng các phương pháp sau:
Bài toán: Cho hình thang ABCD (AB // CD). Gọi M là trung điểm của AD, N là trung điểm của BC. Chứng minh rằng MN // AB // CD.
Lời giải:
Để đạt hiệu quả cao nhất khi giải bài 3 trang 74 Vở thực hành Toán 8, học sinh cần:
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa và vở thực hành Toán 8. Chúng tôi hy vọng sẽ giúp các em học sinh học tập môn Toán một cách hiệu quả và đạt kết quả tốt nhất. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Dạng bài tập | Phương pháp giải |
|---|---|
| Chứng minh tính chất hình học | Sử dụng định lý, tính chất đã học, lập luận logic |
| Tính độ dài, góc | Áp dụng định lý Pitago, hệ thức lượng, tính chất góc |
| Xác định vị trí tương đối | Sử dụng phương pháp tọa độ, vector |