Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 90 Vở thực hành Toán 8 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, giúp các em nắm vững kiến thức và đạt kết quả tốt trong môn Toán.
Bảng sau đây cho biết số lượng học sinh giỏi cấp tỉnh các môn Toán
Đề bài
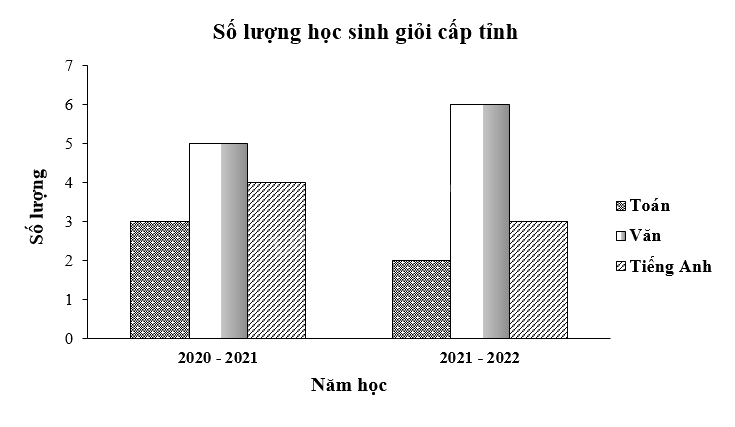
Bảng sau đây cho biết số lượng học sinh giỏi cấp tỉnh các môn Toán, Văn, Tiếng Anh của một trường THCS trong hai năm học.

Lựa chọn và vẽ biểu đồ để so sánh số lượng học sinh giỏi cấp tỉnh các môn Toán, Văn, Tiếng Anh trong mỗi năm học.
Phương pháp giải - Xem chi tiết
Dựa vào bảng thống kê, lựa chọn biểu đồ phù hợp và vẽ.
Lời giải chi tiết
Ta sử dụng biểu đồ cột bội để biểu diễn như sau:
Bài 8 trang 90 Vở thực hành Toán 8 thường thuộc các chủ đề về hình học, cụ thể là các kiến thức liên quan đến tứ giác, hình thang, hoặc các tính chất của đường trung bình trong tam giác. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, định lý và tính chất cơ bản của các hình đã học.
Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, cần phân tích mối liên hệ giữa các yếu tố này và tìm ra phương pháp giải phù hợp. Thông thường, các bài toán về hình học đòi hỏi học sinh phải vẽ hình chính xác và sử dụng các định lý, tính chất đã học để chứng minh hoặc tính toán.
Do nội dung bài 8 có thể thay đổi tùy theo từng phiên bản sách Vở thực hành Toán 8, chúng ta sẽ xét một ví dụ minh họa về một dạng bài tập thường gặp:
Cho hình thang ABCD (AB // CD). Gọi M là trung điểm của AD, N là trung điểm của BC. Chứng minh rằng MN = (AB + CD) / 2.
Ngoài dạng bài tập chứng minh đường trung bình của hình thang, bài 8 trang 90 Vở thực hành Toán 8 còn có thể xuất hiện các dạng bài tập khác như:
Đối với các dạng bài tập này, học sinh cần áp dụng linh hoạt các định lý, tính chất đã học và kết hợp với các kỹ năng vẽ hình, phân tích bài toán để tìm ra lời giải chính xác.
Để nắm vững kiến thức và kỹ năng giải bài tập về hình thang và đường trung bình, học sinh nên luyện tập thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các nguồn tài liệu học tập khác. Đồng thời, cần thường xuyên ôn tập lý thuyết và kiểm tra lại các bước giải để đảm bảo tính chính xác và hiệu quả.
Bài 8 trang 90 Vở thực hành Toán 8 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình thang và đường trung bình. Bằng cách nắm vững lý thuyết, phân tích bài toán một cách kỹ lưỡng và luyện tập thường xuyên, các em sẽ có thể giải quyết bài tập này một cách dễ dàng và hiệu quả.