Bài 8 trang 99 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đặc biệt là các định lý liên quan đến tứ giác để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 99 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
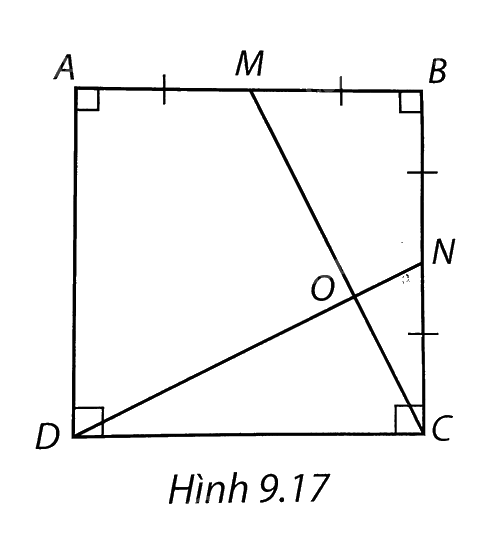
Cho hình vuông ABCD có cạnh bằng 4cm và M, N lần lượt là trung điểm của AB, BC. Gọi O là giao điểm của CM và DN (H.9.17). Tính độ dài đoạn thẳng OM.
Đề bài
Cho hình vuông ABCD có cạnh bằng 4cm và M, N lần lượt là trung điểm của AB, BC.
Gọi O là giao điểm của CM và DN (H.9.17). Tính độ dài đoạn thẳng OM.
Phương pháp giải - Xem chi tiết
Chứng minh CM $\bot $ DN. Tính diện tích tam giác DMN => OM.
Lời giải chi tiết
Ta có $\Delta CBM=\Delta DCN$(hai tam giác vuông có hai cặp cạnh tương ứng bằng nhau).
Do đó $\widehat{CNO}+\widehat{NCO}=\widehat{CND}+\widehat{BCM}=\widehat{BMC}+\widehat{BCM}={{90}^{0}}$.
Vì tổng các góc trong tam giác NOC bằng 1800 nên: $\widehat{NOC}={{180}^{0}}-\widehat{CNO}-\widehat{NCO}={{90}^{0}}$.
Suy ra CM vuông góc với DN.
Gọi S là diện tích hình vuông ABCD. Ta có:
${{S}_{\Delta DMN}}=S-{{S}_{\Delta NBM}}-{{S}_{\Delta MAC}}=16-4-2-4=6(c{{m}^{2}})$.
Do vậy OM. DN = $2{{S}_{\Delta DMN}}$. Suy ra $OM=\frac{2{{S}_{\Delta DMN}}}{\sqrt{C{{D}^{2}}+C{{N}^{2}}}}=\frac{12}{\sqrt{16+4}}=\frac{6\sqrt{5}}{5}(cm)$.
Bài 8 trang 99 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Bài 8 thường yêu cầu chứng minh một tứ giác là một loại tứ giác đặc biệt nào đó. Để làm được điều này, học sinh cần:
(Giả sử đề bài là: Cho tứ giác ABCD có AB = CD, AD = BC. Chứng minh ABCD là hình bình hành.)
Lời giải:
Xét hai tam giác ABD và CDB, ta có:
Do đó, tam giác ABD = tam giác CDB (c-c-c). Suy ra ∠ABD = ∠CDB (hai góc tương ứng).
Ta có ∠ABD + ∠CBD = ∠ABC và ∠CDB + ∠ADB = ∠ADC.
Vì ∠ABD = ∠CDB nên ∠ABC = ∠ADC.
Mà ∠ABC + ∠ADC = 360° (tổng các góc trong một tứ giác) nên ∠ABC = ∠ADC = 180°.
Vậy, tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
Ngoài bài 8 trang 99, Vở thực hành Toán 8 tập 2 còn có nhiều bài tập tương tự về tứ giác. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức về tứ giác, các em học sinh có thể tự giải các bài tập sau:
Bài 8 trang 99 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về tứ giác và các tính chất của nó. Bằng cách nắm vững lý thuyết, phương pháp giải và luyện tập thường xuyên, các em học sinh có thể tự tin giải quyết các bài tập về tứ giác một cách hiệu quả.