Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 55 Vở thực hành Toán 8. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:
Đề bài
Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:
a) AN = CM.
b) \(\widehat {AMC} = \widehat {ANC}.\)
Phương pháp giải - Xem chi tiết
a) Chứng minh tứ giác AMCN là hình bình hành suy ra AN = CM (hai cạnh tương ứng).
b) Dựa vào tính chất của hình bình hành: Trong hình bình hành, hai góc đối bằng nhau.
Lời giải chi tiết
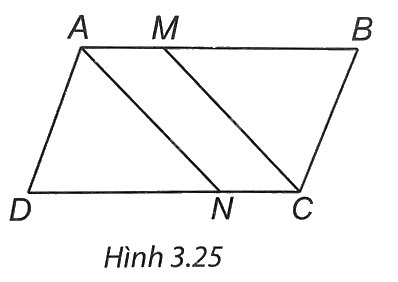
(H.3.25). a) ABCD là hình bình hành ⇒ AB // CD ⇒ AM // CN. Tứ giác AMCN có AM = CN, AM // CN ⇒ AMCN là hình bình hành.
⇒ AN = CM (hai cạnh đối của hình bình hành bằng nhau).
b) AMCN là hình bình hành \( \Rightarrow \widehat {AMC} = \widehat {ANC}\) (hai góc đối của hình bình hành bằng nhau).
Bài 2 trang 55 Vở thực hành Toán 8 thường thuộc các dạng bài tập về phân tích đa thức thành nhân tử, áp dụng các phương pháp như đặt nhân tử chung, sử dụng hằng đẳng thức, nhóm đa thức, và phương pháp tách hạng tử. Việc nắm vững các phương pháp này là chìa khóa để giải quyết hiệu quả các bài toán đại số ở lớp 8.
Để giải bài 2 trang 55 Vở thực hành Toán 8, chúng ta cần xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu phân tích đa thức thành nhân tử hoặc chứng minh một đẳng thức nào đó. Dưới đây là hướng dẫn chi tiết cho từng dạng bài tập thường gặp:
Đây là phương pháp cơ bản nhất. Chúng ta tìm nhân tử chung của tất cả các hạng tử trong đa thức và đặt nó ra ngoài dấu ngoặc. Sau đó, chia mỗi hạng tử cho nhân tử chung để được đa thức còn lại trong ngoặc.
Ví dụ: Phân tích đa thức 3x2 + 6x thành nhân tử.
Sử dụng các hằng đẳng thức đại số để biến đổi đa thức thành nhân tử. Một số hằng đẳng thức thường dùng:
Ví dụ: Phân tích đa thức x2 - 4 thành nhân tử.
Nhóm các hạng tử có chung nhân tử hoặc có thể áp dụng hằng đẳng thức để phân tích. Sau đó, tiếp tục phân tích các nhân tử mới tạo thành.
Ví dụ: Phân tích đa thức ax + ay + bx + by thành nhân tử.
Tách một hạng tử thành tổng hoặc hiệu của các hạng tử khác để tạo ra các nhân tử chung. Phương pháp này thường được sử dụng khi đa thức không dễ dàng phân tích bằng các phương pháp khác.
Bài tập: Phân tích đa thức x2 + 5x + 6 thành nhân tử.
Lời giải:
Việc giải bài 2 trang 55 Vở thực hành Toán 8 đòi hỏi sự hiểu biết về các phương pháp phân tích đa thức và khả năng áp dụng linh hoạt các kiến thức đã học. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.