Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 93 Vở thực hành Toán 8. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho hai biểu đồ (H.5.5).
Đề bài
Cho hai biểu đồ (H.5.5).
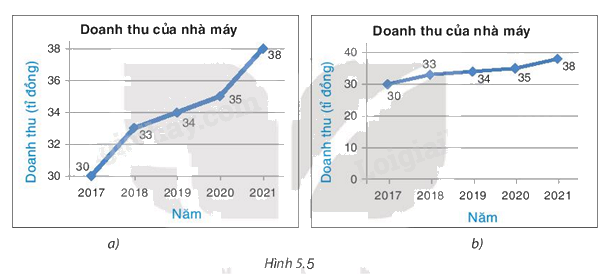
a) Doanh thu của nhà máy trong Biểu đồ a) có tăng nhanh hơn doanh thu của nhà máy trong Biểu đồ b) hay không?
b) Hai biểu đồ này có cùng biểu diễn một dãy số liệu không?
c) Giải thích tại sao hai đường gấp khúc trên hai biểu đồ có độ dốc khác nhau.
Phương pháp giải - Xem chi tiết
Quan sát biểu đồ để đưa ra các nhận xét
Lời giải chi tiết
a) Doanh thu của nhà máy trong Biểu đồ a) tăng nhanh hơn doanh thu của nhà máy trong Biểu đồ b).
b) Hai biểu đồ này cùng biểu diễn một dãy số liệu.
c) Đường gấp khúc trong Biểu đồ a) dốc hơn đường gấp khúc trong Biểu đồ b) là do trục tung ở biểu đồ a) bắt đầu từ 31 và kết thúc tại 38, còn trục tung ở biểu đồ b) bắt đầu ở 0 và kết thúc tại 40.
Bài 2 trang 93 Vở thực hành Toán 8 thuộc chương trình học Toán lớp 8, thường liên quan đến các kiến thức về hình học, cụ thể là các định lý và tính chất của hình thang cân. Việc nắm vững lý thuyết và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn học này.
Bài 2 thường yêu cầu học sinh chứng minh một tính chất nào đó của hình thang cân, hoặc tính toán các yếu tố liên quan đến hình thang cân như độ dài đường trung bình, chiều cao, góc,... Để giải bài tập này, học sinh cần:
Để giúp các em hiểu rõ hơn về cách giải bài 2 trang 93 Vở thực hành Toán 8, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài toán yêu cầu chứng minh rằng đường trung bình của hình thang cân chia hình thang cân thành hai hình thang cân bằng nhau.
Vẽ hình thang cân ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Vẽ đường thẳng MN. Ta cần chứng minh rằng ABMN và MNCD là hai hình thang cân bằng nhau.
Ta có: M là trung điểm của AD, N là trung điểm của BC. Do đó, MN là đường trung bình của hình thang ABCD.
Suy ra: MN = (AB + CD) / 2
Vì MN // AB // CD nên ABMN là hình thang.
Để chứng minh ABMN là hình thang cân, ta cần chứng minh góc MAN = góc ANM.
Ta có: góc MAN = góc ADN (so le trong do MN // CD)
Và góc ANM = góc BCN (so le trong do MN // AB)
Vì ABCD là hình thang cân nên góc ADN = góc BCN.
Suy ra: góc MAN = góc ANM. Vậy ABMN là hình thang cân.
Tương tự như trên, ta có thể chứng minh MNCD là hình thang cân.
Khi giải bài tập về hình thang cân, các em cần chú ý những điều sau:
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, các em có thể tự giải thêm các bài tập tương tự trong sách giáo khoa và vở bài tập. Ngoài ra, các em cũng có thể tham khảo các tài liệu học tập trực tuyến trên giaitoan.edu.vn.
Bài 2 trang 93 Vở thực hành Toán 8 là một bài tập quan trọng giúp các em hiểu sâu hơn về các tính chất của hình thang cân. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.