Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 64 Vở thực hành Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho hình vuông ABCD. Trên cạnh BC lấy điểm N. Từ A kẻ đường thẳng vuông góc với AN cắt đường thẳng CD tại Q.
Đề bài
Cho hình vuông ABCD. Trên cạnh BC lấy điểm N. Từ A kẻ đường thẳng vuông góc với AN cắt đường thẳng CD tại Q. Gọi I là trung điểm của NQ. Gọi M là giao điểm AI và CD. Qua N dựng đường thẳng song song với CD cắt AI tại P. Chứng minh rằng:
a) ∆PIN = ∆MIQ.
b) Tứ giác MNPQ là hình thoi.
Phương pháp giải - Xem chi tiết
a) Chứng minh ∆PIN = ∆MIQ theo trường hợp góc – cạnh – góc.
b) Chứng minh MNPQ là hình bình hành có hai đường chéo PM ⊥ QN nên là hình thoi.
Lời giải chi tiết
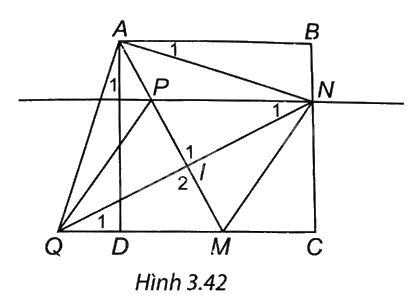
(H.3.42). a) Xét hai tam giác PIN và MIQ có \({\widehat I_1} = {\widehat I_2}\) (hai góc đối đỉnh), QI = IN, \({\widehat N_1} = {\widehat Q_1}\) (do NP // QM)
⇒ ∆PIN = ∆MIQ (g.c.g)
⇒ QM = NP.
b) Tứ giác MNPQ có PN // MQ, QM = NP nên là hình bình hành.
Ta chứng minh MNPQ có hai đường chéo vuông góc.
Vì AQ ⊥ AN nên \({\widehat A_1} + \widehat {DAN} = 90^\circ ,\,\,{\widehat A_2} + \widehat {DAN} = 90^\circ \) Xét hai tam giác vuông ADQ và ABN có AD = AB, \({\widehat A_1} = {\widehat A_2}.\) (chứng minh trên).
⇒ ∆ADQ = ∆ABN (cạnh góc vuông – góc nhọn)
⇒ AQ = AN.
Do đó tam giác AQN cân tại A, mà AI là đường trung tuyến của tam giác AQN
⇒ AI là đường cao của tam giác AQN, tức là AI ⊥ QN, hay PM ⊥ QN.
Hình bình hành MNPQ có hai đường chéo PM ⊥ QN nên là hình thoi.
Bài 5 trang 64 Vở thực hành Toán 8 thường thuộc chương trình học về các phép biến đổi đơn giản với đa thức, hoặc các bài toán liên quan đến phân tích đa thức thành nhân tử. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đa thức, các phép toán cộng, trừ, nhân, chia đa thức, và các phương pháp phân tích đa thức thành nhân tử như đặt nhân tử chung, sử dụng hằng đẳng thức, nhóm đa thức, và phương pháp thêm bớt hạng tử.
Để cung cấp một lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 5 trang 64. Tuy nhiên, dựa trên kinh nghiệm giảng dạy và các đề bài tương tự, chúng ta có thể dự đoán một số dạng bài tập thường gặp:
Các bài tập thuộc dạng này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia đa thức. Để giải quyết, học sinh cần áp dụng các quy tắc về phép toán với đa thức, chú ý đến việc nhóm các hạng tử đồng dạng và sử dụng các tính chất phân phối, kết hợp.
Ví dụ: Thực hiện phép tính (2x + 3)(x - 1)
Lời giải: (2x + 3)(x - 1) = 2x(x - 1) + 3(x - 1) = 2x2 - 2x + 3x - 3 = 2x2 + x - 3
Đây là một trong những dạng bài tập quan trọng trong chương trình Toán 8. Học sinh cần sử dụng các phương pháp phân tích đa thức thành nhân tử để đưa đa thức về dạng tích của các nhân tử.
Ví dụ: Phân tích đa thức x2 - 4 thành nhân tử
Lời giải: x2 - 4 = (x - 2)(x + 2) (Sử dụng hằng đẳng thức a2 - b2 = (a - b)(a + b))
Một số bài tập có thể yêu cầu học sinh vận dụng kiến thức về đa thức để giải quyết các bài toán thực tế. Trong trường hợp này, học sinh cần phân tích bài toán, xây dựng mô hình toán học, và sử dụng các kiến thức đã học để tìm ra lời giải.
Để củng cố kiến thức và kỹ năng, các em có thể tự giải các bài tập tương tự trong Vở thực hành Toán 8 hoặc các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em tự tin hơn khi giải các bài toán khó.
Bài 5 trang 64 Vở thực hành Toán 8 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đa thức và các phép toán với đa thức. Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập trên đây, các em sẽ tự tin hơn khi giải quyết bài toán này và đạt kết quả tốt trong môn Toán.
| Dạng bài | Phương pháp giải |
|---|---|
| Thực hiện phép toán | Áp dụng quy tắc, nhóm hạng tử đồng dạng |
| Phân tích đa thức | Đặt nhân tử chung, hằng đẳng thức, nhóm đa thức |
| Bài toán ứng dụng | Xây dựng mô hình, vận dụng kiến thức |