Bài 5 trang 88 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đặc biệt là các định lý liên quan đến tứ giác để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 88 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat{ABN}=\widehat{ACM}\)
Đề bài
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat{ABN}=\widehat{ACM}\)
a) Chứng minh rằng ΔABN ∽ ΔACM.
b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB.IN = IC.IM.
Phương pháp giải - Xem chi tiết
a) Chứng minh: tam giác ABN và tam giác ACM
có góc A chung, \(\widehat{ABN}=\widehat{ACM}\) => ΔABN ∽ ΔACM
b) Chứng minh: ΔIBM ∽ ΔICN (g.g) nên suy ra các tỉ số đồng dạng
Lời giải chi tiết
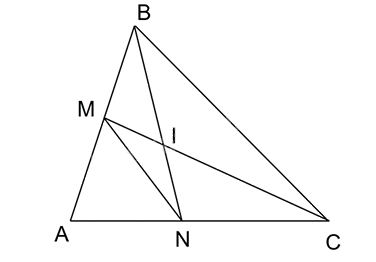
a) Hai tam giác ABN và ACM có: $\widehat{ABN}=\widehat{ACM}$ (theo giả thiết), $\widehat{A}$ chung.
b) Hai tam giác IBM và ICN có:
$\widehat{IBM}=\widehat{ABN}=\widehat{ACM}=\widehat{ICN}$ (theo giả thiết), $\widehat{BIM}=\widehat{CIN}$(hai góc đối đỉnh). Vậy $\Delta IBM\backsim \Delta ICN(g.g)$.
Suy ra $\frac{IB}{IC}=\frac{IM}{IN}$, hay IB.IN = IC.IM.
Bài 5 trang 88 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác, một trong những kiến thức nền tảng của hình học lớp 8. Để giải quyết bài toán này, học sinh cần nắm vững các định nghĩa, tính chất của các loại tứ giác đặc biệt như hình chữ nhật, hình thoi, hình vuông, hình bình hành và các dấu hiệu nhận biết chúng.
Bài 5 thường yêu cầu học sinh chứng minh một tứ giác là một loại tứ giác đặc biệt nào đó dựa trên các thông tin đã cho về độ dài cạnh, góc hoặc đường chéo. Hoặc, bài toán có thể yêu cầu tính độ dài cạnh, góc của một tứ giác khi biết một số yếu tố khác.
Để giải bài 5 trang 88 Vở thực hành Toán 8 tập 2, học sinh có thể áp dụng các phương pháp sau:
Giả sử đề bài yêu cầu chứng minh tứ giác ABCD là hình bình hành, biết AB = CD và AD = BC. Ta có thể giải như sau:
Ngoài dạng bài tập chứng minh tứ giác là một loại tứ giác đặc biệt, bài 5 trang 88 Vở thực hành Toán 8 tập 2 còn có thể xuất hiện các dạng bài tập sau:
Khi giải bài tập về tứ giác, học sinh cần lưu ý những điều sau:
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết cho các môn Toán từ lớp 6 đến lớp 12. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, Giaitoan.edu.vn sẽ giúp các em học sinh học Toán một cách hiệu quả và đạt kết quả cao.
Hãy truy cập Giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và nhận được sự hỗ trợ từ các chuyên gia Toán học!
| Loại tứ giác | Tính chất | Dấu hiệu nhận biết |
|---|---|---|
| Hình bình hành | Hai cạnh đối song song, hai cạnh đối bằng nhau, hai góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường | Tứ giác có hai cạnh đối song song, hoặc hai cạnh đối bằng nhau |
| Hình chữ nhật | Có bốn góc vuông, hai đường chéo bằng nhau | Tứ giác có ba góc vuông, hoặc là hình bình hành có một góc vuông |
| Hình thoi | Bốn cạnh bằng nhau, hai đường chéo vuông góc với nhau | Tứ giác có bốn cạnh bằng nhau, hoặc là hình bình hành có hai cạnh kề bằng nhau |
| Hình vuông | Có bốn góc vuông, bốn cạnh bằng nhau, hai đường chéo bằng nhau và vuông góc với nhau | Tứ giác có ba góc vuông, hoặc là hình chữ nhật có hai cạnh kề bằng nhau, hoặc là hình thoi có một góc vuông |