Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 8. Trang này tập trung vào việc giải các câu hỏi trắc nghiệm trong Vở thực hành Toán 8 tập 2, trang 110. Mục tiêu của chúng tôi là giúp bạn hiểu rõ kiến thức và tự tin làm bài tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi cung cấp các lời giải dễ hiểu, kèm theo các bước giải chi tiết và giải thích rõ ràng.
Chọn phương án đúng trong mỗi câu sau.
Đáy của hình chóp tam giác đều là:
A. Hình vuông.
B. Hình bình hành.
C. Tam giác vuông.
D. Tam giác đều.
Phương pháp giải:
Dựa vào khái niệm của hình chóp tam giác đều.
Lời giải chi tiết:
Đáy của hình chóp tam giác đều là tam giác đều.
=> Chọn đáp án D.
Thể tích của hình chóp tam giác đều bằng:
A. Tích của diện tích đáy với chiều cao của nó.
B. Nửa tích của diện tích đáy với chiều cao của nó.
C. \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
D. Tích của trung đoạn với chu vi đáy.
Phương pháp giải:
Dựa vào công thức tính diện tích hình chóp tam giác đều.
Lời giải chi tiết:
Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
=> Chọn đáp án C.
Một hình chóp tam giác đều có diện tích đáy bằng 30cm2, chiều cao bằng 6cm. Thể tích của hình chóp tam giác đều này bằng:
A. 180cm3.
B. 56cm3.
C. 36cm3.
D. 60cm3.
Phương pháp giải:
Dựa vào công thức tính diện tích hình chóp tam giác đều: Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
Lời giải chi tiết:
Thể tích của hinh chóp tam giác đều đó là: \(V = \frac{1}{3}S.h = \frac{1}{3}.30.6 = 60(c{m^3})\).
=> Chọn đáp án D.
Hình chóp tam giác đều có chu vi đáy bằng 15cm, diện tích xung quanh bằng 30cm2. Độ dài trung đoạn của hình chóp bằng:
A. 4cm.
B. 2cm.
C. 6cm.
D. 8cm.
Phương pháp giải:
Dựa vào công thức tính diện tích của hình chóp tam giác đều để tính độ dài trung đoạn.
Lời giải chi tiết:
Diện tích xung quanh của hinh chóp tam giác đều đó là: \({S_{xq}} = pd \Rightarrow d = \frac{{{S_{xq}}}}{p} = \frac{{30}}{{\frac{{15}}{2}}} = 4(cm)\).
=> Chọn đáp án A.
Một trung đoạn của hình chóp tam giác đều trong hình 10.2 là:
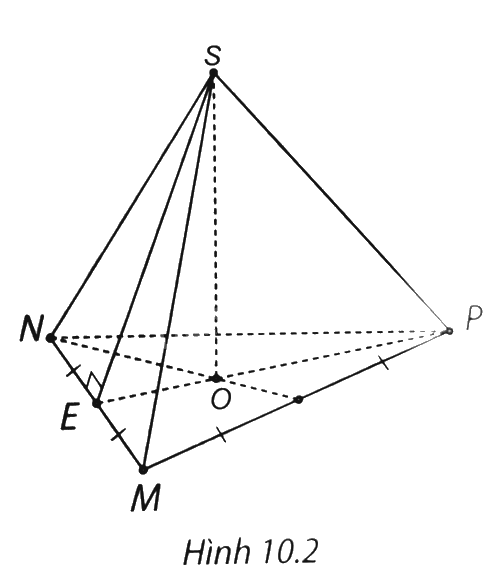
A. SM.
B. SE.
C. MN.
D. SP.
Phương pháp giải:
Quan sát hình vẽ và khái niệm trung đoạn của hình chóp tam giác đều để xác định.
Lời giải chi tiết:
Quan sát hình vẽ, ta thấy SE là trung đoạn của hình chóp tam giác đều trên.
=> Chọn đáp án B.
Chọn phương án đúng trong mỗi câu sau.
Đáy của hình chóp tam giác đều là:
A. Hình vuông.
B. Hình bình hành.
C. Tam giác vuông.
D. Tam giác đều.
Phương pháp giải:
Dựa vào khái niệm của hình chóp tam giác đều.
Lời giải chi tiết:
Đáy của hình chóp tam giác đều là tam giác đều.
=> Chọn đáp án D.
Thể tích của hình chóp tam giác đều bằng:
A. Tích của diện tích đáy với chiều cao của nó.
B. Nửa tích của diện tích đáy với chiều cao của nó.
C. \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
D. Tích của trung đoạn với chu vi đáy.
Phương pháp giải:
Dựa vào công thức tính diện tích hình chóp tam giác đều.
Lời giải chi tiết:
Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
=> Chọn đáp án C.
Một trung đoạn của hình chóp tam giác đều trong hình 10.2 là:

A. SM.
B. SE.
C. MN.
D. SP.
Phương pháp giải:
Quan sát hình vẽ và khái niệm trung đoạn của hình chóp tam giác đều để xác định.
Lời giải chi tiết:
Quan sát hình vẽ, ta thấy SE là trung đoạn của hình chóp tam giác đều trên.
=> Chọn đáp án B.
Một hình chóp tam giác đều có diện tích đáy bằng 30cm2, chiều cao bằng 6cm. Thể tích của hình chóp tam giác đều này bằng:
A. 180cm3.
B. 56cm3.
C. 36cm3.
D. 60cm3.
Phương pháp giải:
Dựa vào công thức tính diện tích hình chóp tam giác đều: Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
Lời giải chi tiết:
Thể tích của hinh chóp tam giác đều đó là: \(V = \frac{1}{3}S.h = \frac{1}{3}.30.6 = 60(c{m^3})\).
=> Chọn đáp án D.
Hình chóp tam giác đều có chu vi đáy bằng 15cm, diện tích xung quanh bằng 30cm2. Độ dài trung đoạn của hình chóp bằng:
A. 4cm.
B. 2cm.
C. 6cm.
D. 8cm.
Phương pháp giải:
Dựa vào công thức tính diện tích của hình chóp tam giác đều để tính độ dài trung đoạn.
Lời giải chi tiết:
Diện tích xung quanh của hinh chóp tam giác đều đó là: \({S_{xq}} = pd \Rightarrow d = \frac{{{S_{xq}}}}{p} = \frac{{30}}{{\frac{{15}}{2}}} = 4(cm)\).
=> Chọn đáp án A.
Trang 110 Vở thực hành Toán 8 tập 2 thường chứa các bài tập trắc nghiệm liên quan đến các kiến thức đã học trong chương. Các dạng bài tập thường gặp bao gồm:
Để giải các câu hỏi trắc nghiệm trang 110 Vở thực hành Toán 8 tập 2 một cách hiệu quả, bạn cần:
Câu 1: Thu gọn đa thức sau: 3x2 + 2x - 5x2 + 7x - 1
Giải:
3x2 + 2x - 5x2 + 7x - 1 = (3x2 - 5x2) + (2x + 7x) - 1 = -2x2 + 9x - 1
Vậy đáp án đúng là -2x2 + 9x - 1.
Để giải các bài tập về đa thức, bạn cần nắm vững các quy tắc cộng, trừ, nhân, chia đa thức. Ngoài ra, bạn cũng cần biết cách sử dụng các hằng đẳng thức để đơn giản hóa biểu thức.
Để phân tích đa thức thành nhân tử, bạn có thể sử dụng các phương pháp như đặt nhân tử chung, dùng hằng đẳng thức, nhóm đa thức. Việc lựa chọn phương pháp phù hợp sẽ giúp bạn giải quyết bài toán một cách nhanh chóng và hiệu quả.
Để giải các bài tập về hình học, bạn cần nắm vững các định lý, tính chất của các hình đã học. Ngoài ra, bạn cũng cần biết cách vẽ hình và sử dụng các công cụ hình học để hỗ trợ việc giải toán.
Để giải phương trình bậc nhất một ẩn, bạn cần thực hiện các phép biến đổi tương đương để đưa phương trình về dạng x = a. Sau đó, bạn có thể kiểm tra lại kết quả bằng cách thay x = a vào phương trình ban đầu.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách giáo khoa, sách bài tập và các trang web học toán online. Việc luyện tập thường xuyên sẽ giúp bạn tự tin hơn khi làm bài kiểm tra.
Hãy luôn chủ động học hỏi, tìm tòi và áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế. Đừng ngại hỏi thầy cô, bạn bè khi gặp khó khăn. Chúc bạn học tập tốt!