Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 50 Vở thực hành Toán 8. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết \(\widehat {ABD} = 30^\circ \), tính số đo góc của hình thang đó.
Đề bài
Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết \(\widehat {ABD} = 30^\circ \), tính số đo góc của hình thang đó.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hai đường thẳng song song và tính chất của hình thang cân để tính số đo góc.
Lời giải chi tiết
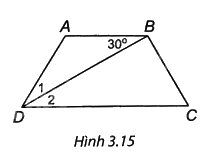
(H.3.15). Tam giác ABD có AB = AD nên ∆ABD cân tại A, do đó \({\widehat D_1} = \widehat {ABD} = 30^\circ .\)
Vì AB // CD nên \({\widehat D_2} = \widehat {ABD} = 30^\circ .\) (hai góc so le trong); suy ra \(\widehat {ADC} = {\widehat D_1} + {\widehat D_2} = 60^\circ .\)
Vì ABCD là hình thang cân nên \(\widehat C = \widehat {ADC} = 60^\circ ,\widehat A = 180^\circ - \widehat {ADC} = 120^\circ = \widehat {ABC}.\)
Bài 2 trang 50 Vở thực hành Toán 8 thường thuộc các dạng bài tập về phân tích đa thức thành nhân tử, áp dụng các phương pháp như đặt nhân tử chung, sử dụng hằng đẳng thức, hoặc nhóm đa thức. Việc nắm vững các kiến thức cơ bản về phân tích đa thức là yếu tố then chốt để giải quyết bài tập này một cách hiệu quả.
Bài 2 trang 50 Vở thực hành Toán 8 thường bao gồm một số câu hỏi yêu cầu phân tích các đa thức sau thành nhân tử:
Để giải bài này, ta sử dụng phương pháp đặt nhân tử chung. Ta thấy rằng cả hai số hạng đều có nhân tử chung là 3x. Do đó:
3x2 - 6x = 3x(x - 2)
Bài này có thể được giải bằng cách sử dụng hằng đẳng thức (a - b)2 = a2 - 2ab + b2. Ta có:
x2 - 4x + 4 = x2 - 2.x.2 + 22 = (x - 2)2
Bài này có thể được giải bằng cách sử dụng hằng đẳng thức a3 + b3 = (a + b)(a2 - ab + b2). Ta có:
x3 + 8 = x3 + 23 = (x + 2)(x2 - 2x + 4)
Bài này có thể được giải bằng cách sử dụng hằng đẳng thức a2 - b2 = (a - b)(a + b). Ta có:
x2 - 25 = x2 - 52 = (x - 5)(x + 5)
Khi giải các bài tập về phân tích đa thức thành nhân tử, các em cần:
Ngoài bài 2 trang 50, các em có thể tham khảo thêm các bài tập tương tự trong Vở thực hành Toán 8 để củng cố kiến thức. Việc hiểu rõ các phương pháp phân tích đa thức sẽ giúp các em giải quyết các bài toán phức tạp hơn trong tương lai.
Xét đa thức: 2x2 + 4x + 2
Ta có thể đặt nhân tử chung là 2:
2x2 + 4x + 2 = 2(x2 + 2x + 1)
Sau đó, nhận thấy x2 + 2x + 1 là một hằng đẳng thức (x + 1)2, ta có:
2(x2 + 2x + 1) = 2(x + 1)2
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên, các em học sinh đã có thể tự tin giải bài 2 trang 50 Vở thực hành Toán 8. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!