Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trắc nghiệm trong Vở thực hành Toán 8. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với các dạng bài tập trắc nghiệm đòi hỏi sự nhanh nhạy và chính xác.
Với mục tiêu hỗ trợ học sinh học tập hiệu quả, chúng tôi đã biên soạn và kiểm tra kỹ lưỡng các lời giải cho từng câu hỏi trắc nghiệm trang 72, 73 Vở thực hành Toán 8.
Chọn phương án đúng trong mỗi câu sau:
Mỗi tam giác có bao nhiêu đường trung bình?
A. 1.
B. 2.
C. 3.
D. 4.
Phương pháp giải:
Dựa vào khái niệm đường trung bình: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Lời giải chi tiết:
Tam giác có 3 cạnh nên tạo được 3 đường trung bình.
=> Chọn đáp án B.
Cho tam giác ABC có chu vi bằng 20 cm. Gọi M, N, P lần lượt là trung điểm của AB, BC, AC. Chu vi tam giác MNP bằng:
A. 20 cm.
B. 10 cm2.
C. 10 cm.
D. 40 cm.
Phương pháp giải:
Áp dụng tính chất đường trung bình: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Chu vi của tam giác bằng tổng ba cạnh của tam giác đó.
Lời giải chi tiết:
Ta có M, N, P lần lượt là trung điểm của AB, BC, AC nên MN, NP, MP đều là đường trung bình của tam giác ABC.
Khi đó BC = 2MP, AB = 2NP, AC = 2MN
Do đó AB + BC + AC = 2(MN + NP + MP)
Vậy MN + NP + MP = 10 (cm).
=> Chọn đáp án C.
Cho ∆ABC đều, cạnh 3 cm; M, N là trung điểm của AB và AC. Chu vi của tứ giác MNCB bằng:
A. 8 cm.
B. 7,5 cm.
C. 6 cm.
D. 7 cm.
Phương pháp giải:
Áp dụng tính chất đường trung bình: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Chu vi của tứ giác bằng tổng bốn cạnh của tứ giác đó.
Lời giải chi tiết:
Ta có M, N là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC nên BC = 2MN.
Khi đó MN = 1,5 cm.
Chu vi của tứ giác MNCB là:
MN + NC + BC + MB = 1,5 + 1,5 + 3 + 1,5 = 7,5 (cm).
=> Chọn đáp án B.
Tìm độ dài x trong Hình 4.10.
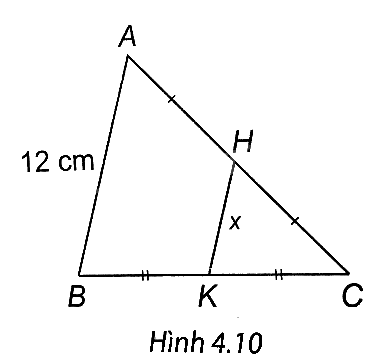
A. 12 cm.
B. 24 cm.
C. 6 cm.
D. 10 cm.
Phương pháp giải:
- Áp dụng khái niệm đường trung bình: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
Ta có: H là trung điểm AC, K là trung điểm BC nên HK là đường trung bình của tam giác ABC.
Suy ra, HK // AB. Áp dụng định lí Thales, ta có \(\frac{{HK}}{{AB}} = \frac{{CH}}{{AC}} = \frac{1}{2}\)
Do đó \(HK = \frac{{AC}}{2} = \frac{{12}}{2} = 6\) (cm).
=> Chọn đáp án C.
Quan sát Hình 4.11 và chọn khảng định đúng.
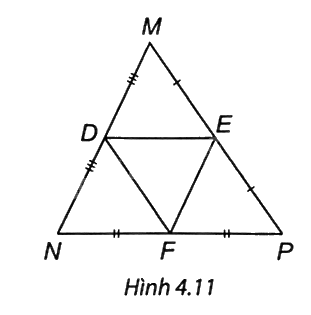
A. DE = NP.
B. DF = 2MP.
C. EF = 2DM.
D. NP = 2DE.
Phương pháp giải:
- Áp dụng khái niệm đường trung bình: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Áp dụng tính chất đường trung bình: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết:
Ta có D là trung điểm MN, E là trung điểm MP, F là trung điểm NP nên DE, EF, DF đều là đường trung bình của tam giác MNP.
Do đó DE // NP, EF // MN, DF // MP và MN = 2EF, NP = 2DE, MP = 2DF.
=> Chọn đáp án D.
Mỗi tam giác có bao nhiêu đường trung bình?
A. 1.
B. 2.
C. 3.
D. 4.
Phương pháp giải:
Dựa vào khái niệm đường trung bình: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Lời giải chi tiết:
Tam giác có 3 cạnh nên tạo được 3 đường trung bình.
=> Chọn đáp án B.
Tìm độ dài x trong Hình 4.10.
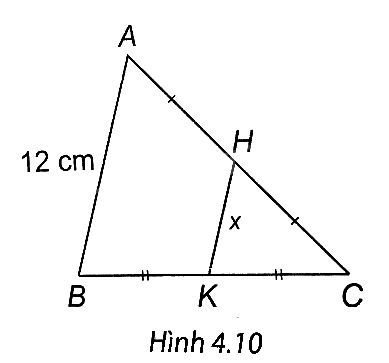
A. 12 cm.
B. 24 cm.
C. 6 cm.
D. 10 cm.
Phương pháp giải:
- Áp dụng khái niệm đường trung bình: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
Ta có: H là trung điểm AC, K là trung điểm BC nên HK là đường trung bình của tam giác ABC.
Suy ra, HK // AB. Áp dụng định lí Thales, ta có \(\frac{{HK}}{{AB}} = \frac{{CH}}{{AC}} = \frac{1}{2}\)
Do đó \(HK = \frac{{AC}}{2} = \frac{{12}}{2} = 6\) (cm).
=> Chọn đáp án C.
Quan sát Hình 4.11 và chọn khảng định đúng.
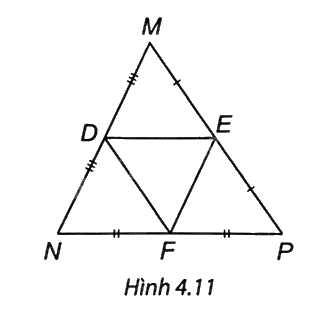
A. DE = NP.
B. DF = 2MP.
C. EF = 2DM.
D. NP = 2DE.
Phương pháp giải:
- Áp dụng khái niệm đường trung bình: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Áp dụng tính chất đường trung bình: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết:
Ta có D là trung điểm MN, E là trung điểm MP, F là trung điểm NP nên DE, EF, DF đều là đường trung bình của tam giác MNP.
Do đó DE // NP, EF // MN, DF // MP và MN = 2EF, NP = 2DE, MP = 2DF.
=> Chọn đáp án D.
Cho tam giác ABC có chu vi bằng 20 cm. Gọi M, N, P lần lượt là trung điểm của AB, BC, AC. Chu vi tam giác MNP bằng:
A. 20 cm.
B. 10 cm2.
C. 10 cm.
D. 40 cm.
Phương pháp giải:
Áp dụng tính chất đường trung bình: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Chu vi của tam giác bằng tổng ba cạnh của tam giác đó.
Lời giải chi tiết:
Ta có M, N, P lần lượt là trung điểm của AB, BC, AC nên MN, NP, MP đều là đường trung bình của tam giác ABC.
Khi đó BC = 2MP, AB = 2NP, AC = 2MN
Do đó AB + BC + AC = 2(MN + NP + MP)
Vậy MN + NP + MP = 10 (cm).
=> Chọn đáp án C.
Cho ∆ABC đều, cạnh 3 cm; M, N là trung điểm của AB và AC. Chu vi của tứ giác MNCB bằng:
A. 8 cm.
B. 7,5 cm.
C. 6 cm.
D. 7 cm.
Phương pháp giải:
Áp dụng tính chất đường trung bình: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Chu vi của tứ giác bằng tổng bốn cạnh của tứ giác đó.
Lời giải chi tiết:
Ta có M, N là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC nên BC = 2MN.
Khi đó MN = 1,5 cm.
Chu vi của tứ giác MNCB là:
MN + NC + BC + MB = 1,5 + 1,5 + 3 + 1,5 = 7,5 (cm).
=> Chọn đáp án B.
Bài tập trắc nghiệm trang 72, 73 Vở thực hành Toán 8 tập trung vào các chủ đề quan trọng như phân thức đại số, quy tắc biến đổi phân thức, và các bài toán ứng dụng liên quan. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là yếu tố then chốt để đạt kết quả tốt trong môn Toán.
Các câu hỏi trắc nghiệm trong trang này thường yêu cầu học sinh:
Để giải quyết hiệu quả các bài tập này, học sinh cần:
Dưới đây là giải chi tiết từng câu hỏi trắc nghiệm trang 72, 73 Vở thực hành Toán 8:
(Nội dung câu hỏi 1)
Lời giải: (Giải thích chi tiết từng bước giải câu hỏi 1, bao gồm cả các bước biến đổi và lý luận toán học. Sử dụng các ký hiệu toán học và giải thích rõ ràng để người đọc dễ hiểu.)
(Nội dung câu hỏi 2)
Lời giải: (Giải thích chi tiết từng bước giải câu hỏi 2, bao gồm cả các bước biến đổi và lý luận toán học. Sử dụng các ký hiệu toán học và giải thích rõ ràng để người đọc dễ hiểu.)
(Nội dung câu hỏi 3)
Lời giải: (Giải thích chi tiết từng bước giải câu hỏi 3, bao gồm cả các bước biến đổi và lý luận toán học. Sử dụng các ký hiệu toán học và giải thích rõ ràng để người đọc dễ hiểu.)
Để đạt hiệu quả cao trong việc giải bài tập trắc nghiệm Toán 8, bạn có thể áp dụng một số mẹo sau:
Phân thức không chỉ là một khái niệm toán học trừu tượng mà còn có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập trắc nghiệm mà chúng tôi cung cấp, bạn sẽ tự tin hơn trong việc học tập môn Toán 8. Hãy luyện tập thường xuyên và áp dụng kiến thức đã học vào thực tế để đạt kết quả tốt nhất. Chúc bạn học tập hiệu quả!