Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 81 Vở thực hành Toán 8. Bài viết này sẽ giúp các em hiểu rõ cách giải bài tập, nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các bài giải chuẩn xác, dễ hiểu và phương pháp giải khoa học.
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G.
Đề bài
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất đường trung bình của tam giác.
Lời giải chi tiết
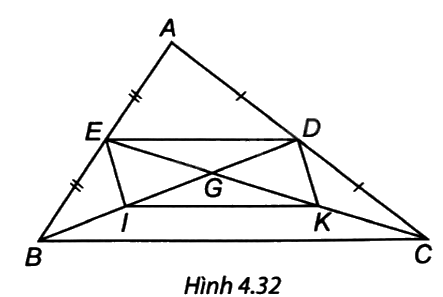
∆ABC có: E là trung điểm AB, D là trung điểm AC nên ED là đường trung bình của ∆ABC. Suy ra ED // BC và ED = \(\frac{1}{2}\)BC. (1)
∆GBC có: I là trung điểm GC, K là trung điểm GB nên IK là đường trung bình của ∆GBC. Suy ra IK // BC và IK = \(\frac{1}{2}\)BC. (2)
Từ (1) và (2) suy ra ED // IK và ED = IK nên tứ giác EDKI là hình bình hành.
Bài 6 trang 81 Vở thực hành Toán 8 thuộc chương trình học Toán lớp 8, thường liên quan đến các kiến thức về hình học, cụ thể là các định lý và tính chất của hình thang cân. Bài tập yêu cầu học sinh vận dụng các kiến thức đã học để chứng minh các tính chất, tính toán độ dài đoạn thẳng, góc hoặc diện tích hình.
Để giải quyết bài 6 trang 81 Vở thực hành Toán 8 một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Để giải bài 6 trang 81 Vở thực hành Toán 8, các em có thể thực hiện theo các bước sau:
Bài toán: Cho hình thang cân ABCD (AB // CD). Gọi M là trung điểm của AD, N là trung điểm của BC. Chứng minh rằng MN là đường trung bình của hình thang ABCD.
Lời giải:
Vì M là trung điểm của AD và N là trung điểm của BC nên AM = MD và BN = NC.
Xét tam giác ADC, M là trung điểm của AD và MN cắt DC tại I. Áp dụng định lý Thales, ta có: DI/IC = AM/MC. Tương tự, xét tam giác BCD, N là trung điểm của BC và MN cắt DC tại I. Áp dụng định lý Thales, ta có: DI/IC = BN/ND.
Do đó, DI/IC = AM/MC = BN/ND. Vì AB // CD nên AM // BN. Suy ra, MN là đường trung bình của hình thang ABCD.
Các bài tập trong bài 6 trang 81 Vở thực hành Toán 8 thường xoay quanh các dạng sau:
Để giải các bài tập về hình thang cân một cách hiệu quả, các em nên:
Bài 6 trang 81 Vở thực hành Toán 8 là một bài tập quan trọng giúp các em củng cố kiến thức về hình thang cân. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải quyết bài tập và đạt kết quả tốt trong môn Toán.