Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 58 Vở thực hành Toán 8. Bài học này thuộc chương trình Toán 8, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến hình học.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và lời giải dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
Đề bài
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
a) Hỏi tứ giác MPAN là hình gì?
b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?
Phương pháp giải - Xem chi tiết
a) Chứng minh tứ giác MPAN có 3 góc vuông nên là hình chữ nhật.
b) Dựa vào tính chất đường trung tuyến của tam giác vuông.
Lời giải chi tiết
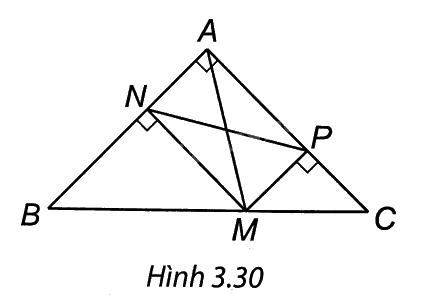
(H.3.30). a) Tứ giác MPAN có góc vuông tại A, P, N nên là một hình chữ nhật.
b) Vì MPAN là hình chữ nhật nên NP = AM.
Với điểm M tùy ý trên BC, H là chân đường cao hạ từ A của tam giác ABC, khi đó ta có AM ≥ AH.
Vậy AM nhỏ nhất khi AM = AH, tức khi M trùng H (với H là trung điểm của BC do tam giác ABC vuông cân tại A).
Do đó NP ngắn nhất khi M là trung điểm của BC.
Bài 4 trang 58 Vở thực hành Toán 8 thường xoay quanh các kiến thức về tứ giác, đặc biệt là các loại tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi, hình vuông. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất và dấu hiệu nhận biết của từng loại tứ giác.
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài 4 trang 58. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một số hướng giải quyết phổ biến:
Nếu đề bài yêu cầu chứng minh một tứ giác ABCD là hình bình hành, ta có thể sử dụng một trong các cách sau:
Nếu đề bài cho biết một số thông tin về hình bình hành (ví dụ: độ dài một cạnh, một góc), ta có thể sử dụng các tính chất của hình bình hành để tính các yếu tố còn lại.
Diện tích hình bình hành được tính bằng công thức: S = a * h (trong đó a là độ dài đáy và h là chiều cao tương ứng).
Để củng cố kiến thức và kỹ năng giải bài tập về tứ giác và hình bình hành, các em có thể tự giải các bài tập sau:
Để học tốt môn Toán, các em cần:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập này, các em sẽ học tốt môn Toán 8 và đạt kết quả cao trong các kỳ thi.