Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 67 Vở thực hành Toán 8. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C.
Đề bài
Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E, K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N, D lần lượt là chân đường vuông góc hạ từ B xuống MEvà từ M xuống AB (H.3.46).
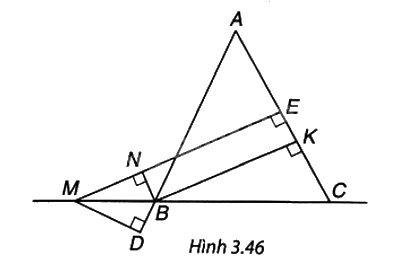
Chứng minh rằng:
a) Tứ giác BKEN là hình chữ nhật.
b) BK bằng hiệu khoảng cách từ M đến AC và đến AB (dù M thay đổi trên đường thẳng BC miễn là B nằm giữa M và C) tức là BK = ME – MD.
Phương pháp giải - Xem chi tiết
a) Chứng minh BKEN có ba góc vuông nên là hình chữ nhật.
b) Dựa vào tính chất của hình chữ nhật, tam giác cân, tam giác vuông để chứng minh.
Lời giải chi tiết
a) Tứ giác BKEN có ba góc vuông N, E, K nên là hình chữ nhật.
b) Tứ giác BKEN là hình chữ nhật nên NE = BK, BN // EK.
⇒ \(\widehat {NBM} = \widehat {KCB}\) (hai góc đồng vị). (1)
Ta có \(\widehat {MBD} = \widehat {CBK}\) (hai góc đối đỉnh). (2)
Theo giả thiết, tam giác ABC cân tại A ⇒ \(\widehat {ACB} = \widehat {ABC}\) (3).
Từ (1), (2), (3) suy ra \(\widehat {NBM} = \widehat {DBM}\)
Hai tam giác vuông NBM và DBM có: DB là cạnh chung, \(\widehat {NBM} = \widehat {DBM}\) (chứng minh trên) nên ∆NBM = ∆DBM (cạnh huyền – góc nhọn) ⇒ MN = MD.
Ta có ME – MD = ME – MN = NE = BK (điều phải chứng minh).
Bài 7 trang 67 Vở thực hành Toán 8 thuộc chương trình học Toán lớp 8, tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đại số, đặc biệt là các hằng đẳng thức đáng nhớ. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài 7 thường bao gồm các dạng bài tập sau:
Để phân tích đa thức thành nhân tử, chúng ta có thể sử dụng các phương pháp sau:
Ví dụ: Phân tích đa thức 2x2 + 4x thành nhân tử.
Giải:
2x2 + 4x = 2x(x + 2)
Để rút gọn biểu thức đại số, chúng ta cần thực hiện các phép toán cộng, trừ, nhân, chia các đơn thức và đa thức một cách chính xác. Lưu ý sử dụng các quy tắc về dấu và thứ tự thực hiện các phép toán.
Ví dụ: Rút gọn biểu thức (x + 2)(x - 2) + x2.
Giải:
(x + 2)(x - 2) + x2 = x2 - 4 + x2 = 2x2 - 4
Để tính giá trị của biểu thức đại số tại một giá trị cụ thể của biến, chúng ta thay giá trị đó vào biểu thức và thực hiện các phép toán.
Ví dụ: Tính giá trị của biểu thức 3x2 - 2x + 1 tại x = 2.
Giải:
3(2)2 - 2(2) + 1 = 3(4) - 4 + 1 = 12 - 4 + 1 = 9
Để chứng minh đẳng thức, chúng ta cần biến đổi một vế của đẳng thức thành vế còn lại. Có thể sử dụng các phương pháp như phân tích đa thức thành nhân tử, rút gọn biểu thức, hoặc sử dụng các hằng đẳng thức.
Ví dụ: Chứng minh đẳng thức (a + b)2 = a2 + 2ab + b2.
Giải:
(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2
Bài 7 trang 67 Vở thực hành Toán 8 là một bài tập quan trọng giúp các em củng cố kiến thức về các phép biến đổi đại số. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.