Bài 4 trang 48 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đại số để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 48 VTH Toán 8 tập 2, giúp các em học sinh hiểu rõ bản chất bài toán và rèn luyện kỹ năng giải toán.
Cho hàm số y = (m – 1)x – m + 4. a) Vẽ đồ thị của hàm số khi m = -2.
Đề bài
Cho hàm số y = (m – 1)x – m + 4.
a) Vẽ đồ thị của hàm số khi m = -2.
b) Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.
c) Tìm giá trị của m để đồ thị hàm số đã cho đi qua điểm (2; -3).
Phương pháp giải - Xem chi tiết
a) Thay m = -2 vào hàm số, xác định hai điểm thuộc đồ thị hàm số đó để vẽ đồ thị hàm số.
b) Dựa vào khái niệm hàm số bậc nhất: Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó a, b là các số cho trước và a ≠ 0.
c) Thay điểm (2; -3) vào hàm số để tìm m.
Lời giải chi tiết
a) Thay m = -2, ta được y = (-2 – 1)x – (-2) + 4 => y = -3x + 6.
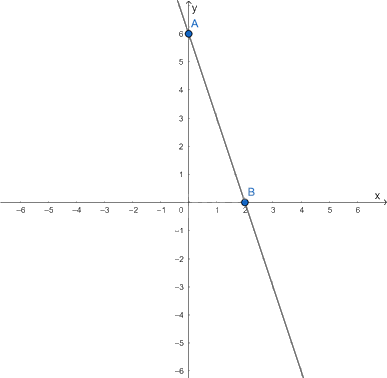
Cho x = 0 thì y = 6, ta được giao điểm của đồ thị với trục Oy là A(0; 6).
Cho y = 0 thì x = 2, ta được giao điểm của đồ thị với trục Ox là B(2; 0).
Kẻ đường thẳng đi qua hai điểm A và B, ta được đồ thị của hàm số y = -3x + 6 như hình bên:
b) Hàm số đã cho là hàm bậc nhất khi m – 1 ≠ 0, tức là m ≠ 1.
c) Vì đồ thị hàm số đi qua điểm (2; -3) nên ta có:
-3 = (m – 1).2 –m + 4
-3 = 2m – 2 – m + 4
m = -5
Vậy m = - 5.
Bài 4 trang 48 Vở thực hành Toán 8 tập 2 thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, đặc biệt là các tính chất của hình thang cân. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi bắt tay vào giải bài toán, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, cần phân tích mối liên hệ giữa các yếu tố này và tìm ra hướng giải quyết phù hợp. Thông thường, để giải bài toán về hình thang cân, học sinh có thể sử dụng các phương pháp sau:
(Giả sử đề bài là: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = BC = 6cm. Tính chiều cao của hình thang.)
Lời giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Khi đó, AH = BK là chiều cao của hình thang.
Vì ABCD là hình thang cân nên DH = KC = (CD - AB) / 2 = (10 - 5) / 2 = 2.5cm.
Xét tam giác vuông ADH, ta có: AH2 + DH2 = AD2 (theo định lý Pitago).
Suy ra: AH2 = AD2 - DH2 = 62 - 2.52 = 36 - 6.25 = 29.75.
Vậy, AH = √29.75 ≈ 5.45cm.
Kết luận: Chiều cao của hình thang ABCD là khoảng 5.45cm.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể tự giải các bài tập tương tự sau:
Khi giải bài tập về hình thang cân, học sinh cần lưu ý những điều sau:
Bài 4 trang 48 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình thang cân và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin giải quyết bài toán này một cách hiệu quả.