Giải bài 2 trang 111 Vở thực hành Toán 8 tập 2

Giải bài 2 trang 111 vở thực hành Toán 8 tập 2

Giải bài 2 trang 111 Vở thực hành Toán 8 tập 2

Bài 2 trang 111 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các định lý và tính chất đã học vào giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 111 Vở thực hành Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.

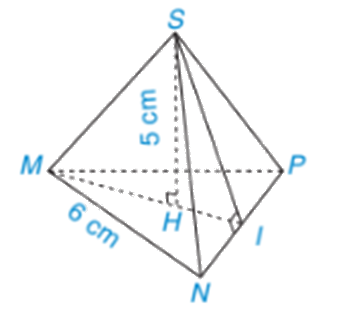
Cho hình chóp tam giác đều S.MNP có độ dài cạnh đáy băng 6cm, chiều cao bằng 5cm. (H.10.4)

Đề bài

Cho hình chóp tam giác đều S.MNP có độ dài cạnh đáy băng 6cm, chiều cao bằng 5cm. (H.10.4)

a) Tính diện tích tam giác MNP.

b) Tính thể tích hình chóp S.MNP, biết \(\sqrt {27} \approx 5,2\)

Giải bài 2 trang 111 vở thực hành Toán 8 tập 2 1

Phương pháp giải - Xem chi tiết Giải bài 2 trang 111 vở thực hành Toán 8 tập 2 2

Áp dụng công thức tính diện tích xung quanh và thể tích của hình chóp tam giác đều.

Lời giải chi tiết

a) NI = 3cm, \(\Delta MNI\) vuông tại I nên theo định lí Pythagore ta có MI² + IN² = MN² hay MI² + 32² = 6², do đó MI² = 6² – 3².

Vậy MI² = 27. Suy ra MI = \(\sqrt {27} \) cm.

Diện tích \(\Delta MNP\) là:

\({S_{MNP}} = \frac{1}{2}MI.NP = \frac{1}{2}.5,2.6 = 15,6(c{m^2})\).

b) Thể tích hình chóp S.MNP là:

\(V = \frac{1}{3}S.h = \frac{1}{3}.15,6.5 = 26(c{m^3})\).

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 2 trang 111 vở thực hành Toán 8 tập 2 đặc sắc thuộc chuyên mục giải toán 8 trên toán math. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 2 trang 111 Vở thực hành Toán 8 tập 2: Tóm tắt lý thuyết và phương pháp giải

Bài 2 trang 111 Vở thực hành Toán 8 tập 2 thường liên quan đến việc áp dụng các định lý về hình thang cân, hình bình hành, hoặc các tính chất của đường trung bình trong tam giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:

Định lý về hình thang cân: Hình thang cân là hình thang có hai cạnh bên bằng nhau. Các góc ở đáy của hình thang cân bằng nhau.
Tính chất của đường trung bình trong tam giác: Đường trung bình của tam giác song song với cạnh thứ ba và bằng một nửa cạnh thứ ba.
Các tính chất của hình bình hành: Các cạnh đối song song và bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Lời giải chi tiết bài 2 trang 111 Vở thực hành Toán 8 tập 2

Để cung cấp lời giải chính xác, cần biết nội dung cụ thể của bài 2 trang 111. Tuy nhiên, dưới đây là một ví dụ về cách tiếp cận giải một bài tập tương tự:

Ví dụ: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = BC = 6cm. Tính chiều cao của hình thang.

Vẽ đường cao AH và BK (H, K thuộc CD).
Chứng minh tam giác ADH bằng tam giác BCK (cạnh huyền - cạnh góc vuông).
Suy ra DH = KC.
Tính DH = (CD - AB) / 2 = (10 - 5) / 2 = 2.5cm.
Áp dụng định lý Pitago trong tam giác ADH để tính chiều cao AH: AH = √(AD² - DH²) = √(6² - 2.5²) = √(36 - 6.25) = √29.75 ≈ 5.45cm.

Các dạng bài tập thường gặp và phương pháp giải

Ngoài dạng bài tập tính chiều cao, bài 2 trang 111 Vở thực hành Toán 8 tập 2 có thể xuất hiện các dạng bài tập sau:

Chứng minh một hình là hình thang cân: Sử dụng các định lý và tính chất của hình thang cân để chứng minh.
Tính độ dài các cạnh của hình thang cân: Áp dụng các định lý và tính chất của hình thang cân, kết hợp với các tam giác đồng dạng (nếu có).
Tính diện tích hình thang cân: Sử dụng công thức diện tích hình thang: S = (a + b)h / 2, trong đó a và b là độ dài hai đáy, h là chiều cao.

Mẹo giải bài tập hình học hiệu quả

Để giải các bài tập hình học nói chung và bài 2 trang 111 Vở thực hành Toán 8 tập 2 nói riêng một cách hiệu quả, học sinh nên:

Vẽ hình chính xác: Hình vẽ chính xác giúp học sinh hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
Nắm vững các định lý và tính chất: Việc nắm vững các kiến thức cơ bản là nền tảng để giải quyết các bài tập.
Sử dụng các công cụ hỗ trợ: Compa, thước kẻ, eke có thể giúp học sinh vẽ hình chính xác và kiểm tra các tính chất hình học.
Luyện tập thường xuyên: Luyện tập thường xuyên giúp học sinh rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập khác nhau.

Bài tập tương tự để luyện tập

Để củng cố kiến thức và kỹ năng giải bài tập, học sinh có thể tham khảo các bài tập tương tự sau:

Bài 1 trang 111 Vở thực hành Toán 8 tập 2
Bài 3 trang 111 Vở thực hành Toán 8 tập 2
Các bài tập trong sách giáo khoa Toán 8 tập 2

Kết luận

Bài 2 trang 111 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán hình học. Bằng cách nắm vững các kiến thức cơ bản, áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, học sinh có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.