Bài 3 trang 102 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 102 VTH Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
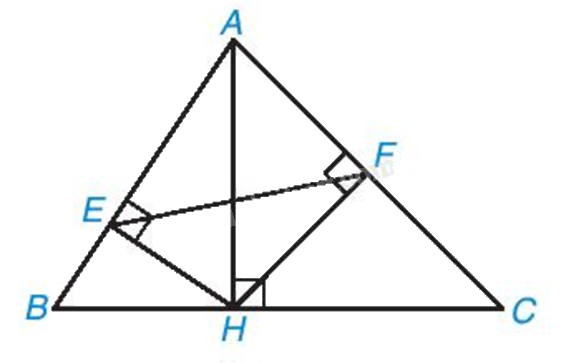
Trong hình 9.22, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng
Đề bài
Trong hình 9.22, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng
a) ΔAEH ∽ ΔAHB
b) ΔAFH ∽ ΔAHC
c) ΔAFE ∽ ΔABC
Phương pháp giải - Xem chi tiết
Sử dụng các trường hợp đồng dạng của tam giác vuông và tam giác thường.
Lời giải chi tiết
a) Hai tam giác vuông AEH (vuông tại E) và AHB (vuông tại H) có $\widehat{EAH}=\widehat{HAB}$ (góc chung). Do đó $\Delta AEH\backsim \Delta AHB$ (một cặp góc nhọn bằng nhau).
b) Hai tam giác vuông AFH (vuông tại F) và AHC (vuông tại H) có $\widehat{FAH}=\widehat{HAC}$ (góc chung). Do đó $\Delta AFH\backsim \Delta AHC$ (một cặp góc nhọn bằng nhau).
c) Vì $\Delta AEH\backsim \Delta AHB$ nên \(\frac{AE}{AC}=\frac{AE}{AH}.\frac{AH}{AC}=\frac{AH}{AB}.\frac{AH}{AC}=\frac{A{{H}^{2}}}{AB.AC}\) (1)
Vì $\Delta AFH\backsim \Delta AHC$ nên \(\frac{AF}{AB}=\frac{AF}{AH}.\frac{AH}{AB}=\frac{AH}{AC}.\frac{AH}{AB}=\frac{A{{H}^{2}}}{AB.AC}\) (2)
Từ (1) và (2) suy ra $\frac{AE}{AC}=\frac{AF}{AB}$.
Hai tam giác AFE và ABC có $\widehat{A}$ chung; $\frac{AE}{AC}=\frac{AF}{AB}$ (Theo chứng minh trên).
Do đó \(\Delta AFE\backsim \Delta ABC\) (c.g.c).
Bài 3 trang 102 Vở thực hành Toán 8 tập 2 thuộc chương trình đại số, thường liên quan đến các kiến thức về phân thức đại số, các phép toán trên phân thức, hoặc các bài toán ứng dụng liên quan đến phân thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc liên quan.
Thông thường, bài 3 trang 102 VTH Toán 8 tập 2 sẽ bao gồm một hoặc nhiều câu hỏi yêu cầu học sinh:
Để giải bài 3 trang 102 VTH Toán 8 tập 2, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Rút gọn phân thức \frac{x^2 - 4}{x + 2}
Giải:
Ta có: \frac{x^2 - 4}{x + 2} = \frac{(x - 2)(x + 2)}{x + 2} = x - 2 (với x \neq -2)
Việc giải bài 3 trang 102 VTH Toán 8 tập 2 không chỉ giúp học sinh nắm vững kiến thức về phân thức đại số mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế. Đây là những kỹ năng quan trọng không chỉ trong môn Toán mà còn trong các môn học khác và trong cuộc sống.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong sách giáo khoa và vở thực hành Toán 8. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em học toán hiệu quả và đạt kết quả cao.
| Dạng bài tập | Mục tiêu |
|---|---|
| Rút gọn phân thức | Vận dụng kiến thức về phân tích đa thức thành nhân tử |
| Thực hiện phép toán phân thức | Quy đồng mẫu số, áp dụng các công thức |
| Giải phương trình/bất phương trình | Biến đổi phương trình/bất phương trình về dạng đơn giản |
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin hơn khi giải bài 3 trang 102 Vở thực hành Toán 8 tập 2. Chúc các em học tập tốt!