Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 74 Vở thực hành Toán 8. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G.
Đề bài
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng EI = DK.
Phương pháp giải - Xem chi tiết
- Sử dụng tính chất đường trung bình của tam giác.
- Chứng minh EDKI là hình bình hành suy ra EI = DK.
Lời giải chi tiết
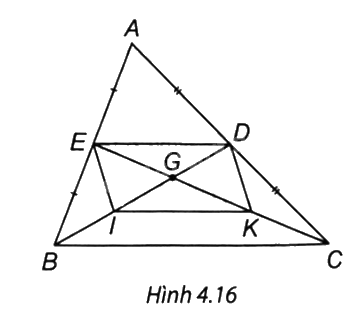
∆ABC có: E là trung điểm AB, D là trung điểm AC, nên DE là đường trung bình của ∆ABC.
Suy ra ED // BC và \(ED = \frac{1}{2}BC\) (tính chất đường trung bình của tam giác). (1)
∆GBC có: I là trung điểm GB, K là trung điểm GC nên IK là đường trung bình của ∆GBC. Suy ra IK // BC và \(IK{\rm{ }} = \frac{1}{2}BC\). (2)
Từ (1) và (2) suy ra: IK // ED, IK = ED.
Tứ giác EDKI có: IK // ED, IK = ED nên tứ giác EDKI là hình bình hành.
Suy ra EI = DK.
Bài 5 trang 74 Vở thực hành Toán 8 thuộc chương trình học Toán lớp 8, thường liên quan đến các kiến thức về hình học, cụ thể là các định lý và tính chất của hình thang cân. Việc nắm vững lý thuyết và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn học này.
Bài 5 trang 74 Vở thực hành Toán 8 thường bao gồm các dạng bài tập sau:
Để giải bài 5 trang 74 Vở thực hành Toán 8 một cách hiệu quả, các em cần:
Bài toán: Cho hình thang cân ABCD (AB // CD), AB = 6cm, CD = 10cm, AD = 5cm. Tính độ dài đường cao của hình thang.
Lời giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Ta có: HK = AB = 6cm. Do đó, DH = KC = (CD - HK) / 2 = (10 - 6) / 2 = 2cm.
Xét tam giác vuông ADH, ta có: AH2 = AD2 - DH2 = 52 - 22 = 21.
Vậy, AH = √21 cm. Do đó, đường cao của hình thang là √21 cm.
Ngoài việc giải bài tập trong Vở thực hành, các em có thể tìm hiểu thêm về các ứng dụng của hình thang cân trong thực tế, như trong kiến trúc, xây dựng, và các lĩnh vực khác. Việc mở rộng kiến thức sẽ giúp các em hiểu sâu hơn về môn Toán và phát triển tư duy logic.
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, các em có thể luyện tập thêm các bài tập tương tự trong sách giáo khoa, sách bài tập, và các trang web học toán online. Giaitoan.edu.vn cung cấp nhiều bài tập và lời giải chi tiết, giúp các em tự tin hơn trong quá trình học tập.
Học Toán đòi hỏi sự kiên trì và luyện tập thường xuyên. Hãy dành thời gian ôn tập lý thuyết, làm bài tập, và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học tốt môn Toán!
| Công thức | Mô tả |
|---|---|
| Diện tích hình thang | S = (a + b)h / 2 (a, b là độ dài hai đáy, h là đường cao) |
| Đường trung bình của hình thang | m = (a + b) / 2 (a, b là độ dài hai đáy) |