Bài 3 trang 87 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đặc biệt là các tính chất của hình thang cân để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 87 Vở thực hành Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA’B’C’ ∽ ΔABC
Đề bài
Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA’B’C’ ∽ ΔABC
Chứng minh rằng \(\frac{{A}'{M}'}{AM}=\frac{{B}'{N}'}{BN}=\frac{{C}'{P}'}{CP}\).
Phương pháp giải - Xem chi tiết
Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để chứng minh.
Lời giải chi tiết
Vì ΔA’B’C’ ∽ ΔABC nên: $\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}$ (1), $\widehat{A'B'C'}=\widehat{ABC},\widehat{B'C'A'}=\widehat{BCA},\widehat{C'A'B'}=\widehat{CAB}$ (2).
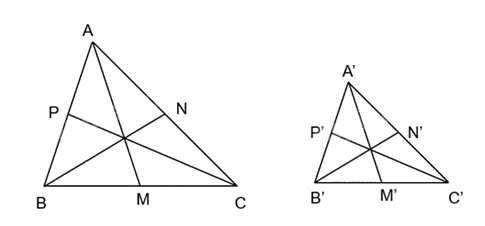
Hai tam giác A’B’M’ và ABM có:
$\frac{B'M'}{BM}=\frac{\frac{B'C'}{2}}{\frac{BC}{2}}=\frac{B'C'}{BC}=\frac{B'A'}{BA}$ (theo (1)),
$\widehat{A'B'M'}=\widehat{A'B'C'}=\widehat{ABC}=\widehat{ABM}$
Suy ra $\Delta A'B'M'\backsim \Delta ABM$(c.g.c). Do đó $\frac{A'M'}{AM}=\frac{A'B'}{AB}$.
Tương tự, \(\Delta B'C'N'\backsim \Delta BCN\) và suy ra $\frac{B'N'}{BN}=\frac{B'C'}{BC},\Delta C'A'P'\backsim \Delta CAP$ và suy ra $\frac{C'P'}{CP}=\frac{A'C'}{AC}$. Từ các đẳng thức trên và (1) ta suy ra $\frac{A'M'}{AM}=\frac{B'N'}{BN}=\frac{C'P'}{CP}$.
Bài 3 trang 87 Vở thực hành Toán 8 tập 2 yêu cầu chúng ta xét hình thang cân ABCD (AB // CD, AD = BC) và tìm các góc của hình thang khi biết một góc nhọn. Bài toán này đòi hỏi học sinh phải hiểu rõ các tính chất của hình thang cân, đặc biệt là mối quan hệ giữa các góc trong hình thang cân.
Để giải bài toán này, chúng ta cần sử dụng các kiến thức sau:
Giả sử: ∠A = 60° (ví dụ)
Yêu cầu: Tính ∠B, ∠C, ∠D
Giải:
Kết luận: ∠B = 60°, ∠C = 120°, ∠D = 120°.
Ngoài bài 3 trang 87, Vở thực hành Toán 8 tập 2 còn có nhiều bài tập tương tự về hình thang cân. Để giải các bài tập này, học sinh cần nắm vững các kiến thức sau:
Bài tập: Cho hình thang cân ABCD (AB // CD, AD = BC). Biết ∠A = 80°. Tính ∠B, ∠C, ∠D.
Lời giải:
Kết luận: ∠B = 80°, ∠C = 100°, ∠D = 100°.
Khi giải bài tập về hình thang cân, học sinh cần chú ý các điểm sau:
Bài 3 trang 87 Vở thực hành Toán 8 tập 2 là một bài tập cơ bản về hình thang cân. Việc nắm vững các kiến thức và kỹ năng giải bài tập này sẽ giúp học sinh tự tin hơn trong việc học Toán 8 và giải quyết các bài toán phức tạp hơn trong tương lai. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về bài toán này và đạt kết quả tốt trong học tập.