Giải bài 5 trang 54 Vở thực hành Toán 8

Giải bài 5 trang 54 vở thực hành Toán 8

Giải bài 5 trang 54 Vở thực hành Toán 8

Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 54 Vở thực hành Toán 8. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.

Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD.

Đề bài

Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh ∆OAM = ∆OCN. Từ đó suy ra tứ giác MBND là hình bình hành.

Phương pháp giải - Xem chi tiết Giải bài 5 trang 54 vở thực hành Toán 8 1

Chứng minh ∆OAM = ∆OCN theo trường hợp góc – cạnh – góc.

Dựa vào dấu hiệu nhận biết tứ giác có hai đường chéo cắt nhau tại trung điểm là hình bình hành, ta chứng minh được MBND là hình bình hành.

Lời giải chi tiết

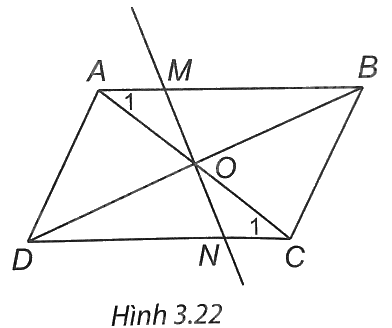
Giải bài 5 trang 54 vở thực hành Toán 8 2

(H.3.22). ABCD là hình bình hành nên AO = CO, BO = DO.

Xét ∆OAM và ∆OCN có: \(\widehat {OAM} = \widehat {OCN}\) (hai góc so le trong), \(\widehat {AOM} = \widehat {CON}\) (hai góc đối đỉnh), AO = CO nên ∆OAM = ∆OCN (g.c.g).

Suy ra OM = ON.

Ta có OM = ON, BO = DO nên tứ giác MBND có hai đường chéo MN, BD cắt nhau tại trung điểm mỗi đường nên MBND là hình bình hành.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 5 trang 54 vở thực hành Toán 8 đặc sắc thuộc chuyên mục toán 8 trên đề thi toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 5 trang 54 Vở thực hành Toán 8: Tổng quan

Bài 5 trang 54 Vở thực hành Toán 8 thuộc chương trình học Toán lớp 8, thường tập trung vào các kiến thức về hình học, cụ thể là các định lý và tính chất liên quan đến tứ giác. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn học này.

Nội dung bài tập

Bài 5 trang 54 Vở thực hành Toán 8 thường bao gồm các dạng bài tập sau:

Chứng minh tính chất của tứ giác: Yêu cầu học sinh chứng minh một tứ giác nào đó là hình bình hành, hình chữ nhật, hình thoi hoặc hình vuông dựa trên các điều kiện cho trước.
Tính độ dài cạnh, số đo góc: Sử dụng các tính chất của tứ giác để tính toán các yếu tố hình học.
Áp dụng tính chất của đường trung bình của tam giác: Liên hệ giữa đường trung bình của tam giác và các yếu tố của tứ giác.
Giải bài toán thực tế: Áp dụng kiến thức về tứ giác để giải quyết các bài toán liên quan đến đời sống.

Hướng dẫn giải chi tiết

Để giải quyết bài 5 trang 54 Vở thực hành Toán 8 một cách hiệu quả, các em cần:

Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán và các dữ kiện đã cho.
Vẽ hình: Vẽ hình minh họa bài toán, giúp hình dung rõ hơn về các yếu tố hình học.
Phân tích bài toán: Xác định các kiến thức và tính chất cần sử dụng để giải bài toán.
Lập luận logic: Sử dụng các kiến thức đã học để lập luận và chứng minh các kết quả.
Kiểm tra lại kết quả: Đảm bảo kết quả cuối cùng là chính xác và hợp lý.

Ví dụ minh họa

Bài tập: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Đường thẳng DE cắt BC tại F. Chứng minh rằng BF = FC.

Lời giải:

Vì ABCD là hình bình hành nên AB // CD và AB = CD.
Vì E là trung điểm của AB nên AE = EB = AB/2.
Xét tam giác AED và tam giác CFD, ta có:

AE = CD (vì AB = CD và AE = AB/2)
∠EAD = ∠DCF (so le trong do AB // CD)
∠AED = ∠CFD (đối đỉnh)

Do đó, tam giác AED = tam giác CFD (g-c-g).
Suy ra DF = ED.
Xét tam giác EBF và tam giác DCF, ta có:

EB = CD (vì AB = CD và EB = AB/2)
∠EBF = ∠DCF (so le trong do AB // CD)
∠BEF = ∠CDF (đối đỉnh)

Do đó, tam giác EBF = tam giác DCF (g-c-g).
Suy ra BF = FC.

Mẹo giải nhanh

Để giải nhanh các bài tập về tứ giác, các em nên:

Nắm vững các định lý và tính chất của các loại tứ giác đặc biệt.
Sử dụng các tính chất của đường trung bình của tam giác một cách linh hoạt.
Vẽ thêm đường phụ để tạo ra các tam giác hoặc hình bình hành quen thuộc.

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài tập, các em nên luyện tập thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các đề thi thử. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với các mức độ khó khác nhau, giúp các em nâng cao khả năng giải toán.

Kết luận

Bài 5 trang 54 Vở thực hành Toán 8 là một bài tập quan trọng giúp các em hiểu sâu hơn về các kiến thức về tứ giác. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.