Bài 9 trang 120 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hình học để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9 trang 120 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin làm bài.
Một khối gỗ gồm đế là hình lập phương cạnh 9 cm và một hình chóp tứ giác đều. Tính thể tích khối gỗ.
Đề bài
Một khối gỗ gồm đế là hình lập phương cạnh 9 cm và một hình chóp tứ giác đều. Tính thể tích khối gỗ.
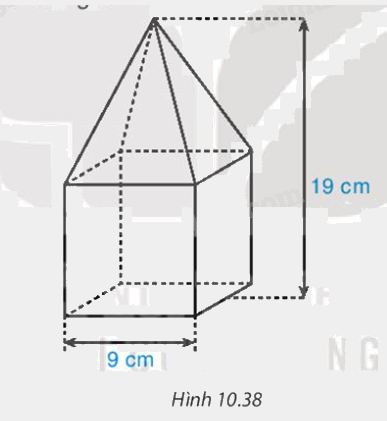
Phương pháp giải - Xem chi tiết
- Tính thể tích của khối chóp.
- Tính thể tích của hình lập phương.
Thể tích của khối gỗ bằng thể tích của khối chóp cộng với thể tích của hình lập phương.
Lời giải chi tiết
Thể tích phần gỗ dạng hình lập phương là:
V1 = 93 = 729 (cm3).
Thể tích phần gỗ có dạng hình chóp tứ giác đều là:
V2 = \(\frac{1}{3}\)(19 – 9).92 = 270 (cm3).
Thể tích khối gỗ là: 729 + 270 = 999 (cm3).
Bài 9 trang 120 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Để giải bài 9 trang 120 Vở thực hành Toán 8 tập 2, chúng ta cần phân tích kỹ đề bài và xác định yêu cầu của bài toán. Sau đó, áp dụng các kiến thức và phương pháp giải phù hợp để tìm ra đáp án chính xác.
(Giả sử đề bài là: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng AF = 2FC.)
Ngoài bài 9 trang 120 Vở thực hành Toán 8 tập 2, còn rất nhiều bài tập tương tự liên quan đến tứ giác. Để giải quyết các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về tứ giác, các em học sinh có thể tham khảo các bài tập sau:
Bài 9 trang 120 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các kiến thức liên quan đến tứ giác. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.