Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 51 Vở thực hành Toán 8. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho AM = AN.
Đề bài
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho AM = AN.
a) Tính số đo góc AMN theo góc A.
b) Tứ giác BMNC là hình gì? Vì sao?
c) Cho BM = MN = NC, chứng minh BN là phân giác của góc ABC, CM là phân giác của góc ACB.
Phương pháp giải - Xem chi tiết
a) Dựa vào tính chất tam giác cân?
b) Sử dụng dấu hiệu nhận biết hình thang cân.
c) Sử dụng tính chất của tam giác cân để chứng minh.
Lời giải chi tiết
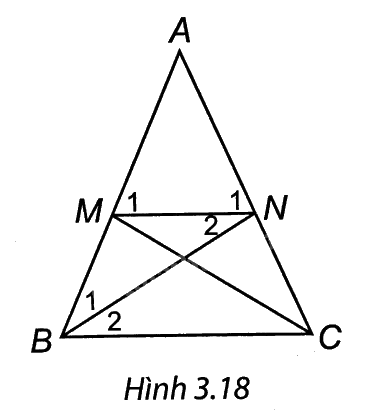
(H.3.18). a) Ta có AM = AN (giả thiết) nên ∆AMN cân tại A
\( \Rightarrow {\widehat M_1} = {\widehat N_1} = \frac{{180^\circ - \widehat A}}{2}.\)
b) Vì ∆ABC cân tại A nên \(\widehat B = \widehat C = \frac{{180^\circ - \widehat A}}{2}.\)
Suy ra \({\widehat M_1} = \widehat B \Rightarrow \) MN // BC (do có cặp góc đồng vị bằng nhau), từ đó tứ giác BMNC là hình thang.
Mặt khác \(\widehat B = \widehat C\) nên BMNC là hình thang cân.
c) Ta có BM = MN ⇒ ∆BMN cân tại M \( \Rightarrow {\widehat B_1} = {\widehat N_2}.\)
Do MN // BC nên \({\widehat B_2} = {\widehat N_2}\) (hai góc so le trong). Từ đó suy ra \({\widehat B_1} = {\widehat B_2},\) tức BN là tia phân giác của góc ABC.
Tương tự ta chứng minh được CM là tia phân giác của góc ACB.
Bài 5 trang 51 Vở thực hành Toán 8 thuộc chương trình học Toán lớp 8, thường tập trung vào các kiến thức về hình học, cụ thể là các định lý và tính chất liên quan đến tứ giác. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn học này.
Bài 5 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 5 trang 51 Vở thực hành Toán 8 một cách hiệu quả, các em cần:
Bài tập: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Đường thẳng DE cắt AC tại I. Chứng minh rằng AI = 2IC.
Lời giải:
Để học tốt môn Toán lớp 8, các em có thể tham khảo các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải bài 5 trang 51 Vở thực hành Toán 8. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!