Giải bài 7 trang 124 Vở thực hành Toán 8 tập 2

Giải bài 7 trang 124 vở thực hành Toán 8 tập 2

Giải bài 7 trang 124 Vở thực hành Toán 8 tập 2

Bài 7 trang 124 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hình học để giải quyết các vấn đề thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7 trang 124 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin làm bài.

Với giá trị nào của m, đường thẳng y = mx + 1 (m ≠ 0)

Đề bài

Với giá trị nào của m, đường thẳng y = mx + 1 (m ≠ 0)

a) Song song với đường thẳng y = 3x?

b) Cắt trục hoành tại điểm có hoành độ bằng -2?

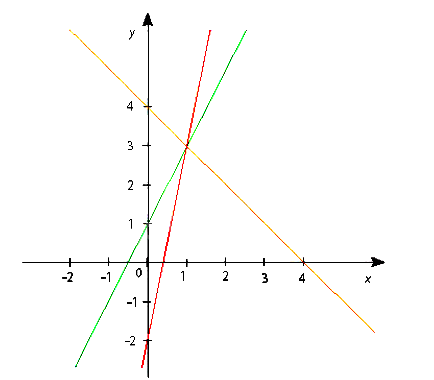
c) Đồng quy với các đường thẳng y = 5x − 2 và y = −x + 4 (tức là ba đường thẳng này cắt nhau tại một điểm)? Với giá trị m tìm được, hãy vẽ ba đường thẳng này trên cùng một hệ trục tọa độ để kiểm nghiệm kết quả.

Phương pháp giải - Xem chi tiết Giải bài 7 trang 124 vở thực hành Toán 8 tập 2 1

a) b) Sử dụng tính chất hai đường thẳng cắt nhau, hai đường thẳng song song.

c) Phương trình hoành độ giao điểm của đường thẳng y = −x + 4 và y = 5x – 2.

Lời giải chi tiết

a) Đường thẳng y = mx + 1 song song với đường thẳng y = 3x khi hai đường thẳng có cùng hệ số góc, tức là m = 3.

b) Đường thẳng y = mx + 1 cắt trục hoành có hoành độ bằng -2, tức là nó đi qua điểm (-2; 0). Điều đó xảy ra khi m.(-2) + 1 = 0, tức là \(m = \frac{1}{2}\).

Trước hết tìm giao điểm của hai đường thẳng y = 5x – 2 và y = -x + 4. Vẽ hai đường thẳng ấy trên cùng một hệ tọa độ (HS tự vẽ):

Trên hình vẽ ta thấy hai đường thẳng cắt nhau tại điểm (1; 3).

Đường thẳng y = mx + 1 đi qua điểm (1; 3) nếu 3 = m + 1. Từ đó suy ra m = 2.

Vậy khi m = 2 thì ba đường thẳng đã cho đồng quy tại điểm (1; 3).

Với m = 2, đồ thị của ba hàm số là ba đường thẳng như hình bên (HS tự vẽ).

Giải bài 7 trang 124 vở thực hành Toán 8 tập 2 2

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 7 trang 124 vở thực hành Toán 8 tập 2 đặc sắc thuộc chuyên mục giải toán 8 trên soạn toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 7 trang 124 Vở thực hành Toán 8 tập 2: Tóm tắt lý thuyết và phương pháp giải

Bài 7 trang 124 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:

Khái niệm tứ giác: Định nghĩa, các loại tứ giác (hình vuông, hình chữ nhật, hình thoi, hình bình hành, hình thang).
Tính chất của các loại tứ giác: Các cạnh đối song song, các góc đối bằng nhau, đường chéo cắt nhau như thế nào.
Dấu hiệu nhận biết các loại tứ giác: Các điều kiện để một tứ giác là hình vuông, hình chữ nhật, hình thoi, hình bình hành, hình thang.

Nội dung bài tập 7 trang 124 Vở thực hành Toán 8 tập 2

Bài tập 7 thường yêu cầu học sinh:

Chứng minh một tứ giác là một loại tứ giác cụ thể (ví dụ: chứng minh một tứ giác là hình bình hành).
Tính độ dài các cạnh, số đo các góc của tứ giác.
Tìm mối quan hệ giữa các yếu tố của tứ giác.
Giải các bài toán thực tế liên quan đến tứ giác.

Hướng dẫn giải bài 7 trang 124 Vở thực hành Toán 8 tập 2 (Ví dụ minh họa)

Đề bài: Cho tứ giác ABCD có AB = CD, AD = BC. Chứng minh tứ giác ABCD là hình bình hành.

Lời giải:

Xét hai tam giác ABD và CDB, ta có:

AB = CD (giả thiết)
AD = BC (giả thiết)
BD là cạnh chung

Do đó, tam giác ABD bằng tam giác CDB (cạnh - cạnh - cạnh). Suy ra ∠ABD = ∠CDB và ∠ADB = ∠CBD.

Vì ∠ABD = ∠CDB (chứng minh trên) mà hai góc này ở vị trí so le trong do AB // CD (giả thiết). Do đó, AB // CD.

Tương tự, vì ∠ADB = ∠CBD (chứng minh trên) mà hai góc này ở vị trí so le trong do AD // BC (giả thiết). Do đó, AD // BC.

Vậy, tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).

Các dạng bài tập thường gặp và phương pháp giải

Ngoài dạng bài chứng minh tứ giác là một loại tứ giác cụ thể, bài tập 7 trang 124 Vở thực hành Toán 8 tập 2 còn có các dạng bài khác như:

Bài tập tính toán: Sử dụng các công thức tính diện tích, chu vi của các loại tứ giác.
Bài tập ứng dụng: Giải các bài toán thực tế liên quan đến tứ giác, ví dụ như tính chiều dài của một con đường, chiều cao của một tòa nhà.

Để giải các bài tập này, học sinh cần:

Vẽ hình chính xác.
Phân tích đề bài để xác định các yếu tố đã cho và yếu tố cần tìm.
Vận dụng các kiến thức đã học về tứ giác để giải bài toán.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Luyện tập thêm

Để nắm vững kiến thức về tứ giác và rèn luyện kỹ năng giải bài tập, học sinh nên làm thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các nguồn tài liệu học tập khác.

Kết luận

Bài 7 trang 124 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.