Bài 5 trang 91 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đại số để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 91 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
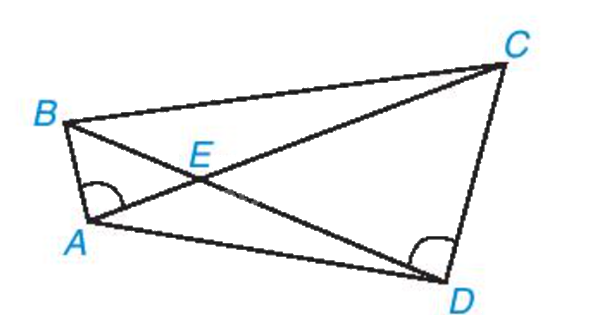
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat{BAC}=\widehat{CDB}\). Chứng minh rằng ΔAED ∽ ΔBEC.
Đề bài
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat{BAC}=\widehat{CDB}\). Chứng minh rằng ΔAED ∽ ΔBEC.
Phương pháp giải - Xem chi tiết
- Chứng minh ΔAEB ∽ ΔDEC suy ra: \(\frac{A\text{E}}{DE}=\frac{BE}{CE}\Rightarrow \frac{A\text{E}}{BE}=\frac{DE}{CF}\)
- Chứng minh ΔAED ∽ ΔBEC (c.g.c)
Lời giải chi tiết
Hai tam giác AEB và DEC có: $\widehat{AEB}=\widehat{DEC}$(hai góc đối đỉnh), $\widehat{BAC}=\widehat{CDB}$ (theo giả thiết).
Vậy $\Delta AEB\backsim \Delta DEC$ (g.g). Suy ra $\frac{EA}{ED}=\frac{EB}{EC}$, hay $\frac{EA}{EB}=\frac{ED}{EC}$.
Hai tam giác AED và BEC có: $\frac{EA}{EB}=\frac{ED}{EC}$ (theo chứng minh trên); $\widehat{AED}=\widehat{BEC}$ (hai góc đối đỉnh). Vậy ΔAED ∽ ΔBEC (c.g.c).
Bài 5 trang 91 Vở thực hành Toán 8 tập 2 thuộc chương trình học Toán 8, tập trung vào việc củng cố kiến thức về các dạng bài tập liên quan đến hình học và đại số. Bài tập này thường yêu cầu học sinh áp dụng các định lý, tính chất đã học để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là rất quan trọng để đạt kết quả tốt trong môn Toán.
Bài 5 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 5 trang 91 Vở thực hành Toán 8 tập 2, chúng tôi xin trình bày lời giải chi tiết cho từng phần của bài tập:
Đề bài: (Ví dụ) Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Lời giải:
Áp dụng định lý Pitago vào tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42 = 9 + 16 = 25
BC = √25 = 5cm
Vậy, độ dài cạnh BC là 5cm.
Đề bài: (Ví dụ) Giải phương trình: 2x + 5 = 11
Lời giải:
2x + 5 = 11
2x = 11 - 5
2x = 6
x = 6 / 2
x = 3
Vậy, nghiệm của phương trình là x = 3.
Đề bài: (Ví dụ) Cho hình chữ nhật ABCD, có AB = 6cm, BC = 8cm. Tính diện tích hình chữ nhật ABCD.
Lời giải:
Diện tích hình chữ nhật ABCD được tính bằng công thức:
Diện tích = AB * BC
Diện tích = 6cm * 8cm = 48cm2
Vậy, diện tích hình chữ nhật ABCD là 48cm2.
Để giải bài tập Toán 8 hiệu quả, các em học sinh cần:
Giaitoan.edu.vn là website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán từ lớp 6 đến lớp 12. Chúng tôi luôn cập nhật nội dung mới nhất, đáp ứng nhu cầu học tập của học sinh. Hãy truy cập Giaitoan.edu.vn để học toán hiệu quả hơn!
| Dạng bài tập | Kiến thức liên quan | Ví dụ |
|---|---|---|
| Tính diện tích hình | Công thức tính diện tích các hình | Tính diện tích hình vuông, hình chữ nhật, hình tam giác |
| Giải phương trình | Các phép biến đổi phương trình | Giải phương trình bậc nhất, bậc hai |
| Chứng minh đẳng thức | Các hằng đẳng thức đại số | Chứng minh (a + b)2 = a2 + 2ab + b2 |