Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 72 Vở thực hành Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập môn Toán, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho hình thang ABCD (AB // DC), AC cắt BD tại I. Chứng minh rằng IA . ID = IB . IC.
Đề bài
Cho hình thang ABCD (AB // DC), AC cắt BD tại I. Chứng minh rằng IA . ID = IB . IC.
Phương pháp giải - Xem chi tiết
Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
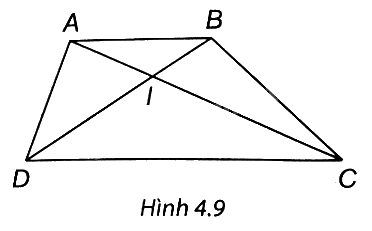
Ta có AB // DC nên theo định lí Thales ta có: \(\frac{{IA}}{{IC}} = \frac{{IB}}{{ID}}\) nên
IA . ID = IB . IC.
Bài 6 trang 72 Vở thực hành Toán 8 thuộc chương trình học Toán lớp 8, thường liên quan đến các kiến thức về hình học, cụ thể là các định lý và tính chất liên quan đến tứ giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và áp dụng linh hoạt các công thức đã học.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải quyết các bài tập trong bài 6 trang 72 Vở thực hành Toán 8, học sinh có thể áp dụng các phương pháp sau:
Bài tập: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Đường thẳng DE cắt AC tại I. Chứng minh rằng AI = IC.
Lời giải:
Khi giải bài tập về tứ giác, học sinh cần chú ý:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo thêm các bài tập sau:
Bài 6 trang 72 Vở thực hành Toán 8 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác. Bằng cách nắm vững các kiến thức cơ bản, áp dụng linh hoạt các phương pháp giải và rèn luyện thường xuyên, các em sẽ có thể giải quyết bài tập một cách dễ dàng và hiệu quả.
Giaitoan.edu.vn hy vọng bài viết này sẽ giúp ích cho các em trong quá trình học tập môn Toán. Chúc các em học tốt!