Bài 8 trang 62 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 62 Vở thực hành Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hàm số bậc nhất y = (m + 2)x + 3 a) Tìm m để đồ thị hàm số song song với đường thẳng y = −x
Đề bài
Cho hàm số bậc nhất y = (m + 2)x + 3
a) Tìm m để đồ thị hàm số song song với đường thẳng y = −x
b) Vẽ đồ thị hàm số với giá trị m tìm được ở câu a
c) Tìm giao điểm A của đồ thị hàm số tìm được ở câu a và đồ thị của hàm số y = x + 1. Tính diện tích của tam giác OAB, trong đó B là giao điểm của đồ thị hàm số y = x + 1 với trục Ox
Phương pháp giải - Xem chi tiết
a) Dựa vào hai đường thẳng song song để tìm giá trị của m.
b, Xác định hai điểm thuộc mỗi đồ thị rồi vẽ đồ thị hàm số.
c) Xác định tọa độ các điểm A, B. Tính AB, OA, OB.
Gọi H là chân đường vuông góc hạ tử A xuống trục hoành.
Tính diện tích tam giác OAB = \(\frac{1}{2}\)AH.OB.
Lời giải chi tiết
a) Đồ thị hàm số song song với đường thẳng y = –x khi m + 2 = −1, tức là m = –3.
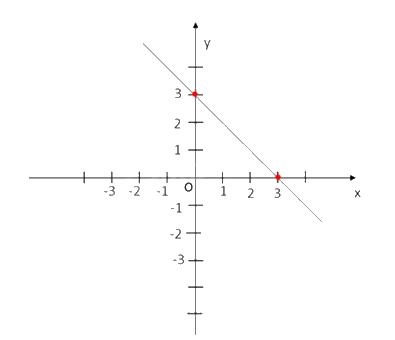
b) Với m = –3, ta có hàm số y = −x + 3. Đồ thị của hàm số này như hình bên.
c)
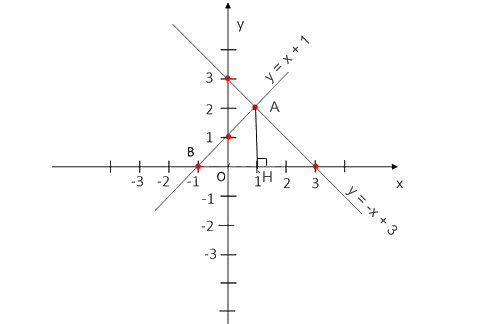
Giao điểm của đồ thị hàm số tìm được ở câu a với đồ thị của hàm số y = x + 1 là A(1; 2).
Giao điểm của đồ thị hàm số y = x + 1 với trục hoành là B(-1; 0).
Do đó OB = 1.
Gọi H là chân đường vuông góc hạ từ A xuống trục hoành. Ta có: H(1, 0) và AH = |yA| = 2.
Diện tích tam giác OAB là SOAB = \(\frac{1}{2}\)AH.OB = \(\frac{1}{2}\).2.1 = 1 (đơn vị diện tích).
Bài 8 trang 62 Vở thực hành Toán 8 tập 2 thuộc chương trình đại số, thường liên quan đến các kiến thức về phân thức đại số, các phép toán trên phân thức, hoặc các bài toán ứng dụng liên quan đến phân thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc liên quan.
Thông thường, bài 8 trang 62 sẽ bao gồm một số câu hỏi hoặc bài tập nhỏ, yêu cầu học sinh thực hiện các thao tác như:
Để giải bài 8 trang 62 Vở thực hành Toán 8 tập 2 một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Rút gọn phân thức \frac{x^2 - 1}{x + 1}
Giải:
\frac{x^2 - 1}{x + 1} = \frac{(x - 1)(x + 1)}{x + 1} = x - 1
Để học tốt Toán 8, học sinh có thể tham khảo các tài liệu sau:
Bài 8 trang 62 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về phân thức đại số. Bằng cách nắm vững kiến thức cơ bản, áp dụng các phương pháp giải hiệu quả và rèn luyện thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự.
| Khái niệm | Giải thích |
|---|---|
| Phân thức đại số | Biểu thức có dạng \frac{P}{Q}, trong đó P và Q là các đa thức, và Q khác 0. |
| Rút gọn phân thức | Chia cả tử và mẫu của phân thức cho một nhân tử chung. |
| Quy đồng mẫu số | Tìm một mẫu số chung của các phân thức, sau đó biến đổi các phân thức để có cùng mẫu số. |