Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 71 Vở thực hành Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB,
Đề bài
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng \(BM = \frac{1}{3}BC.\)
Phương pháp giải - Xem chi tiết
Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
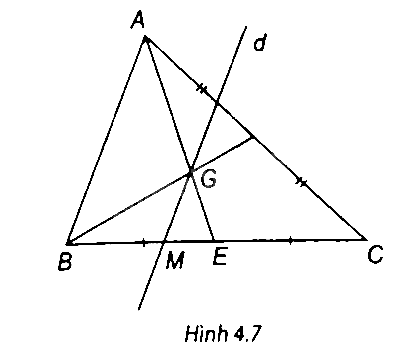
AG cắt BC tại E.
Ta có GM // AB suy ra \(\frac{{BM}}{{BE}} = \frac{{AG}}{{AE}}\) (định lí Thales).
Ta lại có \(\frac{{AG}}{{AE}} = \frac{2}{3}\) (G là trọng tâm ∆ABC) nên \(\frac{{BM}}{{BE}} = \frac{2}{3}.\)
Suy ra \(BM = \frac{2}{3}BE = \frac{2}{3}.\frac{1}{2}BC = \frac{1}{3}BC.\)
AG cắt BC tại E.
Ta có GM // AB suy ra \(\frac{{BM}}{{BE}} = \frac{{AG}}{{AE}}\) (định lí Thales).
Ta lại có \(\frac{{AG}}{{AE}} = \frac{2}{3}\) (G là trọng tâm ∆ABC) nên \(\frac{{BM}}{{BE}} = \frac{2}{3}.\)
Suy ra \(BM = \frac{2}{3}BE = \frac{2}{3}.\frac{1}{2}BC = \frac{1}{3}BC.\)
Bài 4 trang 71 Vở thực hành Toán 8 thuộc chương trình học Toán lớp 8, thường liên quan đến các kiến thức về hình học, cụ thể là các định lý và tính chất của hình thang cân. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và biết cách áp dụng chúng vào thực tế.
Bài 4 thường yêu cầu học sinh chứng minh một tính chất nào đó của hình thang cân, hoặc tính toán các yếu tố liên quan đến hình thang cân như độ dài đường trung bình, chiều cao, góc,...
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 4. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một ví dụ về cách giải:
Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = BC = 6cm. Tính chiều cao của hình thang.
Lời giải:
Ngoài Vở thực hành Toán 8, các em có thể tham khảo thêm sách giáo khoa Toán 8, các bài giảng trực tuyến và các trang web học Toán uy tín để nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải bài 4 trang 71 Vở thực hành Toán 8 một cách hiệu quả. Chúc các em học tập tốt!