Bài 9 trang 80 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9 trang 80 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Bảng sau đây thống kê kết quả khảo sát số người thích một bộ phim mới tại 5 quận A, B, C, D, E của thành phố X
Đề bài
Bảng sau đây thống kê kết quả khảo sát số người thích một bộ phim mới tại 5 quận A, B, C, D, E của thành phố X
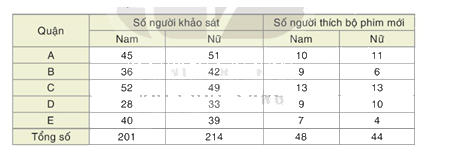
a) Chọn ngẫu nhiên một người ở quận C. Ước lượng xác suất của biến cố:
A: "Người được chọn thích bộ phim đó"
b) Chọn ngẫu nhiên một người ở quận E. Ước lượng xác suất của biến cố:
B: "Người được chọn không thích bộ phim đó"
c) Chọn ngẫu nhiên 600 người ở thành phố X. Ước lượng trong đó có bao nhiêu người thích bộ phim đó
d) Chọn ngẫu nhiên 500 người nữ ở thành phố X. Ước lượng trong đó có bao nhiêu người thích bộ phim đó?
Phương pháp giải - Xem chi tiết
Tính xác suất của biến cố A, B từ đó ước lượng số người thích bộ phim đó.
Lời giải chi tiết
a) Số người ở quận C được khảo sát là 52 + 49 = 101 người, trong đó có 13 + 13 = 6 người thích bộ phim. Vậy xác suất của biến cố A được ước lượng là \(\frac{{26}}{{101}}\).
b) Số người ở quận E được khảo sát là 40 + 39 = 79 người, trong đó có 7 + 4 = 11 người thích bộ phim. Do đó, có 79 – 11 = 68 người không thích bộ phim.Vậy xác suất của biến cố B được ước lượng là \(\frac{{68}}{{79}}\).
c) Gọi C là biến cố “Người được chọn thích bộ phim đó”. Số người ở thành phố X được khảo sát là 201 + 214 = 415 người, trpmg đps cps 48 + 44 = 92 người thích bộ phim. Vậy xác suất của biến cố C được ước lượng P(C) \( \approx \frac{{92}}{{415}}\).
Gọi k là người thích bộ phim. Ta có: P(C) \( \approx \frac{k}{{600}}\). Thay giá trị ước lượng của P(C), ta được \(\frac{k}{{600}} \approx \frac{{92}}{{415}}\), suy ra k \( \approx \frac{{92.600}}{{415}} = 133\). Vậy ta ước lượng có khoảng 133 người thích bộ phim đó trong số 600 người của thành phố X.
d) Gọi D là biến cố “Người nữ được chọn thích bộ phim đó”. Số người nữ ở thành phố X được khảo sát là 214 người, trong đó có 44 người thích bộ phim.
Vậy xác suất của biến cố D được ước lượng là P(D) \( \approx \frac{{44}}{{214}}\).
Gọi h là người thích bộ phim. Ta có P(D) \( \approx \frac{h}{{500}}\). Thay giá trị ước lượng ucar P(D), ta được \(\frac{h}{{500}} \approx \frac{{44}}{{214}}\), suy ra h \( \approx \frac{{44.500}}{{214}} = 103\). Vậy ta ước lượng có khoảng 103 người thích bộ phim đó trong số 500 người nữ của thành phố X.
Bài 9 trang 80 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài tập 9 thường yêu cầu học sinh:
Đề bài: Cho tứ giác ABCD có AB = CD, AD = BC. Chứng minh tứ giác ABCD là hình bình hành.
Lời giải:
Ngoài dạng bài chứng minh tứ giác là hình gì, bài tập 9 trang 80 Vở thực hành Toán 8 tập 2 còn có các dạng bài khác như:
Để giải các bài tập này, học sinh cần:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về tứ giác, học sinh có thể tham khảo thêm các bài tập sau:
Khi giải bài tập về tứ giác, học sinh nên:
Bài 9 trang 80 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 8.