Bạn đang gặp khó khăn trong việc giải các bài tập trắc nghiệm Toán 8 trang 75 và 76 trong Vở thực hành? giaitoan.edu.vn là địa chỉ tin cậy, cung cấp đáp án chi tiết và lời giải dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi hiểu rằng việc làm bài tập trắc nghiệm đòi hỏi sự chính xác và nhanh nhạy. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn bộ giải đáp đầy đủ, giúp bạn hiểu rõ bản chất của từng câu hỏi.
Chọn phương án đúng trong mỗi câu sau:
Quan sát Hình 4.17 và chọn khẳng định đúng.
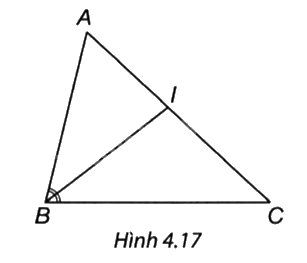
A. \(\frac{{IA}}{{IC}} = \frac{{BA}}{{AC}}.\)
B. \(\frac{{IA}}{{IC}} = \frac{{BC}}{{BA}}.\)
C. \(\frac{{IA}}{{IC}} = \frac{{BA}}{{BC}}.\)
D. \(\frac{{IA}}{{IC}} = \frac{{AC}}{{AB}}.\)
Phương pháp giải:
Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải chi tiết:
Ta có IB là đường phân giác của góc B nên \(\frac{{IA}}{{IC}} = \frac{{AB}}{{BC}}.\)
=> Chọn đáp án C.
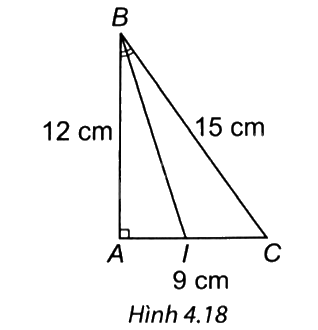
Quan sát Hình 4.18, biết BI là phân giác của góc B, AB = 12 cm, BC = 15 cm, AC = 9 cm. Độ dài đoạn IA là:

A. 5 cm.
B. 4 cm.
C. 6 cm.
D. 3 cm.
Phương pháp giải:
Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải chi tiết:
Ta có BI là phân giác của góc B nên
\(\frac{{IA}}{{AB}} = \frac{{IC}}{{BC}} = \frac{{IA + IC}}{{AB + BC}} = \frac{{AC}}{{AB + BC}} = \frac{9}{{12 + 15}} = \frac{9}{{27}} = \frac{1}{3}\)
Do đó \(IA = \frac{1}{3} \cdot AB = \frac{1}{3} \cdot 12 = 4\) (cm).
=> Chọn đáp án B.
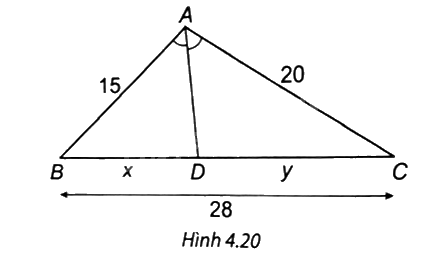
Quan sát Hình 4.20. Độ dài x, y lần lượt là:
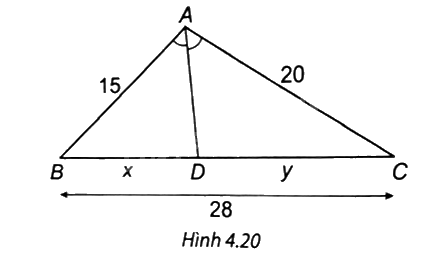
A. x = 16 cm; y = 12 cm.
B. x = 14 cm; y = 14 cm.
C. x = 14,3 cm; y = 10,7 cm.
D. x = 12 cm; y = 16 cm.
Phương pháp giải:
Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải chi tiết:
Ta có AD là phân giác của góc A nên \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).
Khi đó \(\frac{x}{{15}} = \frac{y}{{20}} = \frac{{x + y}}{{15 + 20}} = \frac{{28}}{{35}} = \frac{4}{5}\).
Do đó \(x = \frac{4}{5} \cdot 15 = 12\,\,\left( {cm} \right);y = \frac{4}{5} \cdot 20 = 16\,\,\left( {cm} \right).\)
=> Chọn đáp án D.
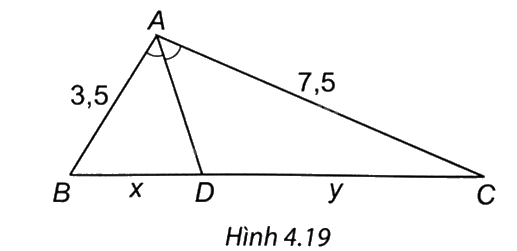
Quan sát Hình 4.19. Tỉ số \(\frac{x}{y}\) bằng
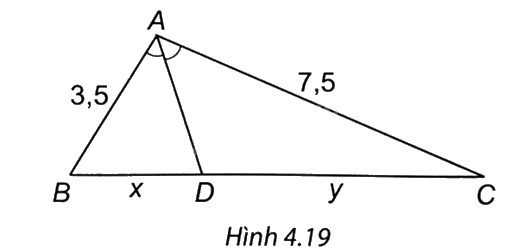
A. \(\frac{1}{7}\).
B. \(\frac{{15}}{7}\)
C. \(\frac{7}{{15}}\)
D. \(\frac{2}{{15}}\)
Phương pháp giải:
Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải chi tiết:
Ta có AD là phân giác của góc A nên \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).
Do đó \(\frac{x}{y} = \frac{{3,5}}{{7,5}} = \frac{7}{{15}}.\)
=> Chọn đáp án C.
Chọn phương án đúng trong mỗi câu sau:
Quan sát Hình 4.17 và chọn khẳng định đúng.
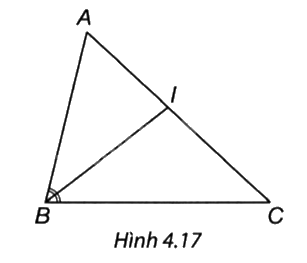
A. \(\frac{{IA}}{{IC}} = \frac{{BA}}{{AC}}.\)
B. \(\frac{{IA}}{{IC}} = \frac{{BC}}{{BA}}.\)
C. \(\frac{{IA}}{{IC}} = \frac{{BA}}{{BC}}.\)
D. \(\frac{{IA}}{{IC}} = \frac{{AC}}{{AB}}.\)
Phương pháp giải:
Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải chi tiết:
Ta có IB là đường phân giác của góc B nên \(\frac{{IA}}{{IC}} = \frac{{AB}}{{BC}}.\)
=> Chọn đáp án C.
Quan sát Hình 4.18, biết BI là phân giác của góc B, AB = 12 cm, BC = 15 cm, AC = 9 cm. Độ dài đoạn IA là:
A. 5 cm.
B. 4 cm.
C. 6 cm.
D. 3 cm.
Phương pháp giải:
Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải chi tiết:
Ta có BI là phân giác của góc B nên
\(\frac{{IA}}{{AB}} = \frac{{IC}}{{BC}} = \frac{{IA + IC}}{{AB + BC}} = \frac{{AC}}{{AB + BC}} = \frac{9}{{12 + 15}} = \frac{9}{{27}} = \frac{1}{3}\)
Do đó \(IA = \frac{1}{3} \cdot AB = \frac{1}{3} \cdot 12 = 4\) (cm).
=> Chọn đáp án B.
Quan sát Hình 4.19. Tỉ số \(\frac{x}{y}\) bằng
A. \(\frac{1}{7}\).
B. \(\frac{{15}}{7}\)
C. \(\frac{7}{{15}}\)
D. \(\frac{2}{{15}}\)
Phương pháp giải:
Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải chi tiết:
Ta có AD là phân giác của góc A nên \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).
Do đó \(\frac{x}{y} = \frac{{3,5}}{{7,5}} = \frac{7}{{15}}.\)
=> Chọn đáp án C.
Quan sát Hình 4.20. Độ dài x, y lần lượt là:
A. x = 16 cm; y = 12 cm.
B. x = 14 cm; y = 14 cm.
C. x = 14,3 cm; y = 10,7 cm.
D. x = 12 cm; y = 16 cm.
Phương pháp giải:
Dựa vào tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải chi tiết:
Ta có AD là phân giác của góc A nên \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).
Khi đó \(\frac{x}{{15}} = \frac{y}{{20}} = \frac{{x + y}}{{15 + 20}} = \frac{{28}}{{35}} = \frac{4}{5}\).
Do đó \(x = \frac{4}{5} \cdot 15 = 12\,\,\left( {cm} \right);y = \frac{4}{5} \cdot 20 = 16\,\,\left( {cm} \right).\)
=> Chọn đáp án D.
Bài tập trắc nghiệm trang 75 và 76 Vở thực hành Toán 8 tập trung vào các chủ đề quan trọng như phân thức đại số, quy tắc biến đổi phân thức, và các bài toán ứng dụng liên quan. Việc nắm vững kiến thức nền tảng là yếu tố then chốt để giải quyết thành công các bài tập này.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích kỹ nội dung của từng bài tập. Xác định rõ yêu cầu của đề bài, các dữ kiện đã cho, và mục tiêu cần đạt được. Điều này giúp bạn lựa chọn phương pháp giải phù hợp và tránh sai sót không đáng có.
Đề bài: Rút gọn biểu thức: (x^2 - 4) / (x + 2)
Lời giải:
Kết luận: Biểu thức được rút gọn là x - 2.
Đề bài: Tìm điều kiện xác định của phân thức: 2x / (x - 3)
Lời giải:
Phân thức xác định khi mẫu số khác 0. Do đó, x - 3 ≠ 0, suy ra x ≠ 3.
Kết luận: Điều kiện xác định của phân thức là x ≠ 3.
Đề bài: Thực hiện phép cộng phân thức: 1/x + 2/x
Lời giải:
Để cộng hai phân thức có cùng mẫu số, ta cộng các tử số và giữ nguyên mẫu số:
1/x + 2/x = (1 + 2) / x = 3/x
Kết luận: Kết quả của phép cộng là 3/x.
Ngoài các bài tập trắc nghiệm cơ bản, trang 75 và 76 Vở thực hành Toán 8 còn xuất hiện một số dạng bài tập nâng cao, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học. Một số dạng bài tập thường gặp bao gồm:
Để giải bài tập trắc nghiệm Toán 8 một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Luyện tập thường xuyên là yếu tố quan trọng để nắm vững kiến thức và kỹ năng giải bài tập trắc nghiệm Toán 8. Hãy dành thời gian giải các bài tập trong sách giáo khoa, vở thực hành, và các đề thi thử để rèn luyện khả năng của mình. Bên cạnh đó, bạn cũng có thể tham gia các khóa học trực tuyến hoặc tìm kiếm sự giúp đỡ từ các giáo viên, bạn bè để nâng cao trình độ.
| Công thức | Mô tả |
|---|---|
| (a/b) * (c/d) = (a*c) / (b*d) | Phép nhân hai phân thức |
| (a/b) / (c/d) = (a/b) * (d/c) | Phép chia hai phân thức |
| (a/b) + (c/b) = (a+c) / b | Phép cộng hai phân thức có cùng mẫu |
| (a/b) - (c/b) = (a-c) / b | Phép trừ hai phân thức có cùng mẫu |
Hy vọng với những giải thích chi tiết và hướng dẫn cụ thể trên đây, bạn sẽ tự tin hơn trong việc giải các câu hỏi trắc nghiệm trang 75, 76 Vở thực hành Toán 8. Chúc bạn học tập tốt!