Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 32 Vở thực hành Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.
Từ một khối lập phương có độ dài cạnh là \(2x + 3\) (cm),
Đề bài
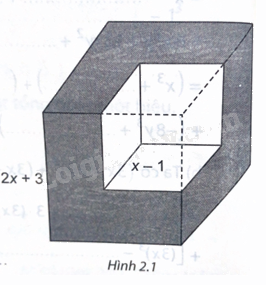
Từ một khối lập phương có độ dài cạnh là \(2x + 3\) (cm), ta cắt bỏ một khối lập phương có độ dài \(x-1\) (cm) (H.2.1). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích khối lập phương.
Lời giải chi tiết
Do cạnh của khối lập phương ban đầu là \(2x + 3\) nên thể tích của khối lập phương ban đầu là \({\left( {2x + 3} \right)^3}\).
Thể tích của khối lập phương bị cắt đi là \({\left( {x-1} \right)^3}\).
Thể tích phần còn lại là \({\left( {2x + 1} \right)^3} - {\left( {x - 1} \right)^3}\)
\(\begin{array}{l} = \left[ {{{\left( {2x} \right)}^3} + 3.{{\left( {2x} \right)}^2}.1 + 3.2x{{.1}^2} + {1^3}} \right] - \left( {{x^3} - 3{x^2} + 3x - 1} \right)\\ = 8{x^3} + 12{x^2} + 6x + 1 - {x^3} + 3{x^2} - 3x + 1\\ = \left( {8{x^3} - {x^3}} \right) + \left( {12{x^2} + 3{x^2}} \right) + \left( {6x - 3x} \right) + \left( {1 + 1} \right)\\ = 7{x^3} + 15{x^2} + 3x + 2.\end{array}\)
Bài 8 trang 32 Vở thực hành Toán 8 thuộc chương trình đại số lớp 8, thường tập trung vào các dạng bài tập liên quan đến phân tích đa thức thành nhân tử, sử dụng các phương pháp như đặt nhân tử chung, sử dụng hằng đẳng thức, hoặc nhóm đa thức. Việc nắm vững kiến thức về phân tích đa thức là nền tảng quan trọng để giải các bài toán phức tạp hơn trong chương trình Toán học.
Để giải quyết bài 8 trang 32 Vở thực hành Toán 8 một cách hiệu quả, chúng ta cần xem xét kỹ đề bài và xác định phương pháp phù hợp. Dưới đây là một số dạng bài tập thường gặp và cách giải chi tiết:
Đây là phương pháp cơ bản nhất để phân tích đa thức thành nhân tử. Chúng ta tìm nhân tử chung của tất cả các hạng tử trong đa thức và đặt nó ra ngoài dấu ngoặc. Ví dụ:
5x2 + 10x = 5x(x + 2)
Có nhiều hằng đẳng thức đại số có thể được sử dụng để phân tích đa thức thành nhân tử. Một số hằng đẳng thức thường gặp bao gồm:
a2 - b2 = (a - b)(a + b)a2 + 2ab + b2 = (a + b)2a2 - 2ab + b2 = (a - b)2a3 + b3 = (a + b)(a2 - ab + b2)a3 - b3 = (a - b)(a2 + ab + b2)Ví dụ: x2 - 4 = (x - 2)(x + 2)
Phương pháp này được sử dụng khi đa thức có nhiều hạng tử. Chúng ta nhóm các hạng tử có chung nhân tử hoặc có thể áp dụng hằng đẳng thức để phân tích.
Ví dụ: x2 + xy + x + y = x(x + y) + (x + y) = (x + 1)(x + y)
Giả sử bài 8 trang 32 yêu cầu phân tích đa thức 2x2 - 8x thành nhân tử. Chúng ta có thể giải như sau:
2x2 và -8x là 2x.2x ra ngoài dấu ngoặc: 2x2 - 8x = 2x(x - 4)Vậy, kết quả phân tích đa thức là 2x(x - 4).
Để củng cố kiến thức và kỹ năng giải bài tập về phân tích đa thức thành nhân tử, các em có thể luyện tập thêm với các bài tập tương tự trong Vở thực hành Toán 8 và các tài liệu tham khảo khác.
Phân tích đa thức thành nhân tử là một kỹ năng quan trọng trong môn Toán học. Nó giúp chúng ta:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải bài 8 trang 32 Vở thực hành Toán 8 một cách hiệu quả. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!