Giải bài 14 trang 108 Vở thực hành Toán 8 tập 2

Giải bài 14 trang 108 vở thực hành Toán 8 tập 2

Giải bài 14 trang 108 Vở thực hành Toán 8 tập 2

Bài 14 trang 108 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hình học để giải quyết các vấn đề thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 14 trang 108 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài.

Cho tam giác nhọn ABC có các đường cao BE, CF cắt nhau tại H. Các đường thẳng qua E, F lần lượt vuông góc và cắt CH, BH tại P, Q. Chứng minh rằng PQ // BC và $\Delta HPQ\backsim \Delta HEF$.

Đề bài

Phương pháp giải - Xem chi tiết Giải bài 14 trang 108 vở thực hành Toán 8 tập 2 1

Chứng minh dựa vào định lí Thales, Thales đảo và các trường hợp đồng dạng của hai tam giác.

Lời giải chi tiết

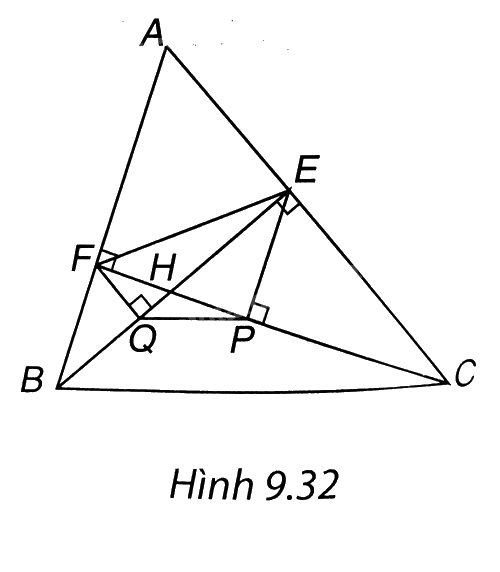
Giải bài 14 trang 108 vở thực hành Toán 8 tập 2 2

(H.9.32). Vì P // BF (cùng vuông góc với CF) nên theo định lí Thales ta có $\frac{HE}{HB}=\frac{HP}{HF}$, hay $HP=\frac{HE.HF}{HB}$.

Tương tự, vì FQ // CE (cùng vuông góc với BE) nên $\frac{HF}{HC}=\frac{HQ}{HE}$, hay $HQ=\frac{HE.HF}{HC}$. Do vậy $\frac{HP}{HQ}=\frac{HC}{HB}$.

Theo định lí Thales đảo ta suy ra PQ // BC.

Mặt khác, hai tam giác vuông BHF (vuông tại F) và CHE (vuông tại E) đồng dạng vì có một cặp góc nhọn bằng nhau là $\widehat{BHF}=\widehat{CHE}$ (hai góc đối đỉnh). Suy ra $\frac{HB}{HC}=\frac{HF}{HE}$.

Do vậy $\frac{HP}{HQ}=\frac{HC}{HB}=\frac{HE}{HF}$.

Hai tam giác HPQ và HEF có: $\frac{HP}{HQ}=\frac{HE}{HF}$ (theo chứng minh trên), $\widehat{PHQ}=\widehat{EHF}$ (hai góc đối đỉnh).

Do đó $\Delta HPQ\backsim \Delta HEF$ (c.g.c).

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 14 trang 108 vở thực hành Toán 8 tập 2 đặc sắc thuộc chuyên mục vở bài tập toán 8 trên tài liệu toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 14 trang 108 Vở thực hành Toán 8 tập 2: Tóm tắt lý thuyết và phương pháp giải

Bài 14 trang 108 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:

Khái niệm tứ giác: Định nghĩa, các loại tứ giác (hình vuông, hình chữ nhật, hình thoi, hình bình hành, hình thang).
Tính chất của các loại tứ giác: Các tính chất liên quan đến cạnh, góc, đường chéo.
Dấu hiệu nhận biết các loại tứ giác: Các dấu hiệu để nhận biết từng loại tứ giác cụ thể.
Ứng dụng của các tính chất và dấu hiệu: Sử dụng các tính chất và dấu hiệu để giải quyết các bài toán liên quan đến tứ giác.

Lời giải chi tiết bài 14 trang 108 Vở thực hành Toán 8 tập 2

Để giải bài 14 trang 108 Vở thực hành Toán 8 tập 2, chúng ta cần phân tích kỹ đề bài và xác định yêu cầu của bài toán. Sau đó, áp dụng các kiến thức và phương pháp giải phù hợp để tìm ra đáp án chính xác.

Đề bài: (Giả sử đề bài là: Cho hình thang ABCD có AB // CD. Gọi M, N lần lượt là trung điểm của AD và BC. Chứng minh rằng MN // AB // CD và MN = (AB + CD)/2)

Lời giải:

Vẽ hình: Vẽ hình thang ABCD với AB // CD, M là trung điểm của AD, N là trung điểm của BC.
Phân tích: Ta cần chứng minh MN // AB // CD và MN = (AB + CD)/2. Để chứng minh MN // AB // CD, ta có thể sử dụng tính chất đường trung bình của tam giác. Để chứng minh MN = (AB + CD)/2, ta có thể sử dụng các tính chất về độ dài đường trung bình và tổng độ dài các cạnh của hình thang.
Chứng minh:
- Xét tam giác ADC, M là trung điểm của AD và N là trung điểm của BC. Do đó, MN là đường trung bình của tam giác ADC.
- Suy ra MN // DC và MN = DC/2.
- Vì AB // DC nên MN // AB // DC.
- Xét tam giác ABC, N là trung điểm của BC và M là trung điểm của AD.
- Kéo dài AM và BN cắt nhau tại I.
- Áp dụng định lý Thales vào tam giác ABI, ta có: AM/AD = BN/BC = 1/2.
- Suy ra MN = (AB + CD)/2.
Kết luận: Vậy MN // AB // CD và MN = (AB + CD)/2.

Các dạng bài tập tương tự và phương pháp giải

Ngoài bài 14 trang 108 Vở thực hành Toán 8 tập 2, còn rất nhiều bài tập tương tự liên quan đến tứ giác. Để giải các bài tập này, học sinh cần:

Nắm vững các định nghĩa, tính chất và dấu hiệu nhận biết các loại tứ giác.
Rèn luyện kỹ năng vẽ hình và phân tích đề bài.
Áp dụng các phương pháp giải phù hợp, như sử dụng tính chất đường trung bình, định lý Thales, các hệ thức lượng trong hình học.
Thực hành giải nhiều bài tập khác nhau để củng cố kiến thức và kỹ năng.

Luyện tập thêm

Để nâng cao khả năng giải toán, các em học sinh có thể luyện tập thêm các bài tập sau:

Bài 15 trang 108 Vở thực hành Toán 8 tập 2
Bài 16 trang 109 Vở thực hành Toán 8 tập 2
Các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác.

Tổng kết

Bài 14 trang 108 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ hiểu rõ hơn về bài toán và tự tin làm bài.