Giải Bài 12 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức

Bài 12 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức

Bài 12 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức: Giải pháp học toán hiệu quả

Bài 12 trang 106 SGK Toán 11 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững phương pháp giải và tự tin làm bài tập.

Hãy cùng khám phá lời giải Bài 12 trang 106 SGK Toán 11 tập 2 ngay bây giờ!

Cho hình hộp (ABCD.A'B'C'D') có đáy ABCD là hình chữ nhật. Biết (AC = AA' = 2a).

Đề bài

Cho hình hộp \(ABCD.A'B'C'D'\) có đáy ABCD là hình chữ nhật. Biết \(AC = AA' = 2a\). Giá trị lớn nhất của thể tích hình hộp \(ABCD.A'B'C'D'\) bằng

A. \(8{a^3}\).

B. \(6{a^3}\).

C. \(4{a^3}\).

D. \({a^3}\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Bài 12 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức 1

Thể tích khối lăng trụ \(V = h.S\)

Lời giải chi tiết

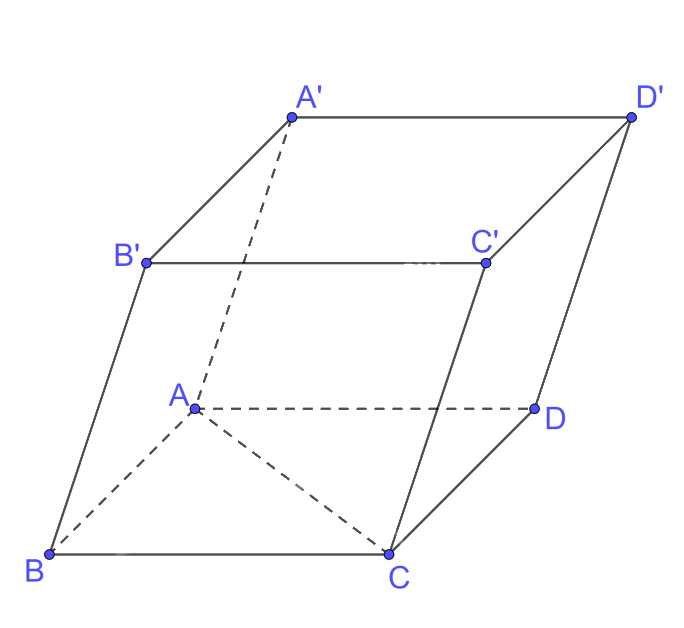
Bài 12 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức 2

Ta có diện tích đáy \(S = AB.AC \le \frac{{A{B^2} + A{C^2}}}{2} = \frac{{A{C^2}}}{2} = \frac{{4{a^2}}}{2} = 2{a^2}\)

Dấu “=” xảy ra khi AB = AC

Chiều cao của hình hộp là \(h = AA'.\sin \left( {AA',\left( {ABCD} \right)} \right) \le AA' = 2a\)

Dấu “=” xảy ra khi \(\left( {AA',\left( {ABCD} \right)} \right) = {90^0}\)

Thể tích của hình hộp là \(V = h.S \le 2a.2{a^2} = 4{a^3}\)

Dấu “=” xảy ra khi \(ABCD.A'B'C'D'\) là hình hộp đứng có đáy là hình vuông.

Đáp án C

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 12 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức – hành trang không thể thiếu trong chuyên mục Sách bài tập Toán 11 trên nền tảng tài liệu toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 12 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức: Giải chi tiết và hướng dẫn

Bài 12 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến khảo sát hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức sau:

Đạo hàm của hàm số: Định nghĩa, ý nghĩa hình học và vật lý của đạo hàm.
Các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
Ứng dụng của đạo hàm: Khảo sát hàm số (xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn).

Nội dung bài tập Bài 12 trang 106 SGK Toán 11 tập 2

Bài 12 thường bao gồm các dạng bài tập sau:

Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của một hàm số cho trước.
Khảo sát hàm số: Yêu cầu xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn của hàm số.
Giải phương trình, bất phương trình: Sử dụng đạo hàm để giải các phương trình, bất phương trình liên quan đến hàm số.
Ứng dụng đạo hàm vào thực tế: Giải các bài toán thực tế liên quan đến tối ưu hóa.

Giải chi tiết Bài 12 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức

Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài. (Phần này sẽ chứa lời giải chi tiết cho từng câu hỏi của bài 12, ví dụ:)

Ví dụ: Giải câu a) Bài 12 trang 106

Câu a) yêu cầu tính đạo hàm của hàm số f(x) = x³ - 3x² + 2. Ta có:

f'(x) = 3x² - 6x

Vậy, đạo hàm của hàm số f(x) là f'(x) = 3x² - 6x.

Ví dụ: Giải câu b) Bài 12 trang 106

Câu b) yêu cầu khảo sát hàm số f(x) = x³ - 3x² + 2. Ta thực hiện các bước sau:

Xác định tập xác định: Tập xác định của hàm số là R.
Tính đạo hàm: f'(x) = 3x² - 6x
Tìm điểm dừng: Giải phương trình f'(x) = 0, ta được x = 0 và x = 2.
Khảo sát dấu của đạo hàm:
x -∞ 0 2 +∞
f'(x) + - +
f(x) Đồng biến Nghịch biến Đồng biến
Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.

x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	Đồng biến	Nghịch biến	Đồng biến

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm và ứng dụng của đạo hàm, bạn có thể luyện tập thêm các bài tập tương tự trong SGK Toán 11 tập 2 - Kết nối tri thức và các tài liệu tham khảo khác.