Bài 7.39 trang 65 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cho tứ diện ABCD có tam giác ABC cân tại (A)
Đề bài
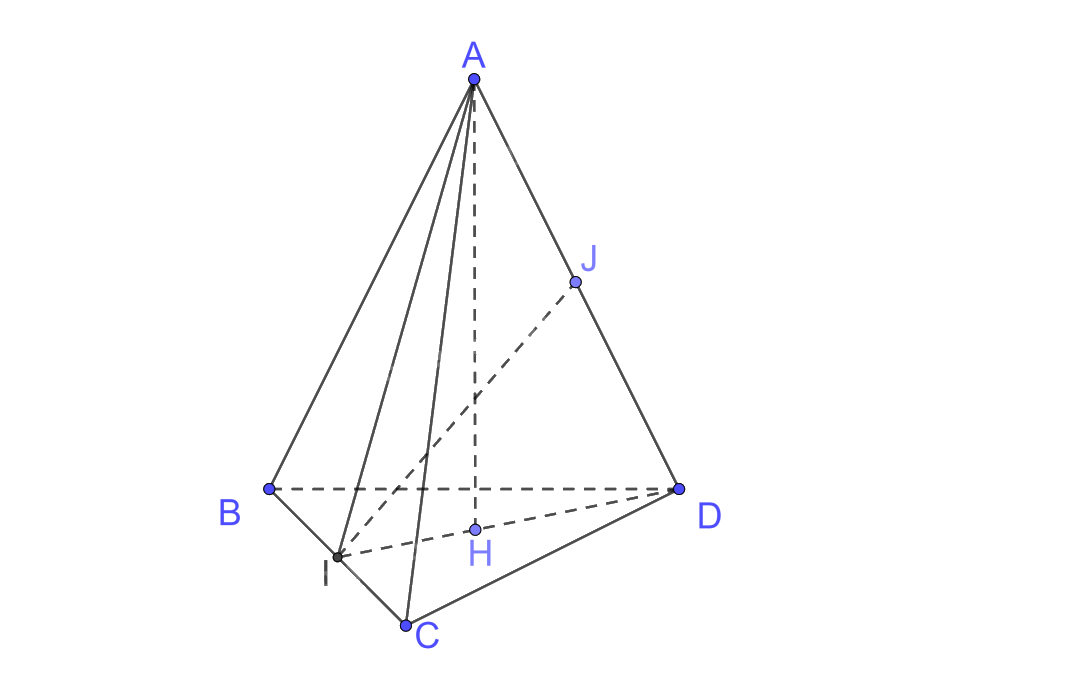
Cho tứ diện ABCD có tam giác ABC cân tại \(A\), tam giác BCD cân tại \(D\). Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng \(BC \bot (AID)\).
b) Kẻ đường cao AH của tam giác AID. Chứng minh rằng \(AH \bot (BCD)\).
c) Kẻ đường cao IJ của tam giác AID. Chứng minh rằng IJ là đường vuông góc chung của AD và BC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
- Hai mặt phẳng vuông góc nếu trong mặt phẳng này có một đường thẳng vuông góc vào giao tuyến thì đường thẳng đó vuông góc với mặt phẳng còn lại.
- Đường thẳng \(\Delta \) cắt hai đường thẳng chéo nhau a, b và vuông góc với cả hai đường thẳng đó được gọi là đường vuông góc chung của a và b.
Lời giải chi tiết
a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC
Bài 7.39 trang 65 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này thường yêu cầu học sinh áp dụng các kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của một đại lượng.
Bài 7.39 thường có dạng như sau: Một vật chuyển động theo phương trình s(t) = ... (trong đó s là quãng đường, t là thời gian). Yêu cầu là tìm vận tốc và gia tốc của vật tại một thời điểm cụ thể.
Giả sử vật chuyển động theo phương trình s(t) = t3 - 3t2 + 5t + 2.
Để tìm vận tốc và gia tốc tại thời điểm t = 2, ta thay t = 2 vào các công thức trên:
Vậy, vận tốc của vật tại thời điểm t = 2 là 5 đơn vị quãng đường/thời gian, và gia tốc của vật tại thời điểm t = 2 là 6 đơn vị quãng đường/thời gian2.
Khi giải bài tập về đạo hàm, cần chú ý đến các quy tắc đạo hàm cơ bản như đạo hàm của hàm số lũy thừa, đạo hàm của tổng, hiệu, tích, thương của các hàm số. Ngoài ra, cần kiểm tra kỹ đơn vị của các đại lượng để đảm bảo kết quả chính xác.
Kiến thức về đạo hàm có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như vật lý, kỹ thuật, kinh tế. Ví dụ, đạo hàm được sử dụng để tính vận tốc, gia tốc của các vật thể chuyển động, để tìm điểm cực trị của hàm số chi phí, lợi nhuận trong kinh tế.
Để củng cố kiến thức về đạo hàm, học sinh có thể làm thêm các bài tập tương tự trong SGK Toán 11 tập 2 - Kết nối tri thức, hoặc tìm kiếm trên các trang web học toán online uy tín.
Bài 7.39 trang 65 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về đạo hàm và ứng dụng của nó. Bằng cách nắm vững phương pháp giải và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và áp dụng kiến thức vào thực tế.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh học tập tốt hơn môn Toán 11.