Bài 3.2 trang 61 SGK Toán 11 tập 1 thuộc chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, đặc biệt là các phép biến đổi lượng giác để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Số sản phẩm một công nhân làm được trong một ngày được cho như sau: 18 25 39 12 54 27 46 25 19 9 36 22 20 19 17 44 5 18 23 28 25 34 46 27 16 Hãy chuyển mẫu số liệu sang dạng ghép nhóm với sau nhóm có độ dài bằng nhau
Đề bài
Số sản phẩm một công nhân làm được trong một ngày được cho như sau:
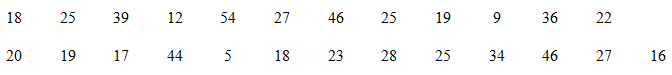
Hãy chuyển mẫu số liệu sang dạng ghép nhóm với sáu nhóm có độ dài bằng nhau.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Để chuyển mẫu số liệu không ghép nhóm sang mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1: Chia miền giá trị của mẫu số liệu thành một số nhóm theo tiêu chí cho trước.
Bước 2: Đếm số giá trị của mẫu số liệu thuộc mỗi nhóm (tần số) và lập bảng thống kê cho mẫu số liệu ghép.
Lời giải chi tiết
Giá trị nhỏ nhất là: 5.
Giá trị lớn nhất là 54.
Do đó khoảng biến thiên là 54 - 5 = 49.
Để chia thành 6 nhóm với độ dài bằng nhau ta lấy điểm đầu mút phải trái của nhóm đầu tiên là 3 và đầu mút phải của nhóm cuối cùng là 57 với độ dài mỗi nhóm là 9.
Ta được mẫu số liệu ghép nhóm như sau:

Bài 3.2 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này tập trung vào việc vận dụng các kiến thức về hàm số lượng giác, bao gồm các phép biến đổi lượng giác, để giải quyết các bài toán thực tế.
Bài tập 3.2 yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để chứng minh đẳng thức lượng giác, ta cần sử dụng các công thức lượng giác cơ bản và các phép biến đổi tương đương. Ví dụ, ta có thể sử dụng công thức cộng và hiệu lượng giác, công thức nhân đôi, công thức hạ bậc để biến đổi vế trái của đẳng thức thành vế phải, hoặc ngược lại.
Ví dụ, để chứng minh đẳng thức sin2x + cos2x = 1, ta có thể sử dụng định lý Pythagoras trong tam giác vuông. Hoặc, để chứng minh đẳng thức tan x = sin x / cos x, ta có thể sử dụng định nghĩa của hàm tan và hàm sin, cos.
Để tính giá trị của biểu thức lượng giác, ta cần thay các giá trị của x vào biểu thức và thực hiện các phép tính. Tuy nhiên, trước khi thay giá trị, ta cần đảm bảo rằng các giá trị của x nằm trong miền xác định của biểu thức.
Ví dụ, để tính giá trị của biểu thức sin(π/3), ta biết rằng sin(π/3) = √3/2. Hoặc, để tính giá trị của biểu thức cos(π/4), ta biết rằng cos(π/4) = √2/2.
Để giải phương trình lượng giác, ta cần sử dụng các công thức lượng giác và các phép biến đổi tương đương để đưa phương trình về dạng đơn giản hơn. Sau đó, ta có thể tìm ra các nghiệm của phương trình.
Ví dụ, để giải phương trình sin x = 0, ta biết rằng x = kπ, với k là số nguyên. Hoặc, để giải phương trình cos x = 1, ta biết rằng x = 2kπ, với k là số nguyên.
Kiến thức về hàm số lượng giác và các phép biến đổi lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực của khoa học và kỹ thuật, bao gồm:
Hy vọng rằng lời giải chi tiết và hướng dẫn giải bài 3.2 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức của Giaitoan.edu.vn sẽ giúp các em học sinh hiểu rõ hơn về bài học và đạt kết quả tốt trong kỳ thi.