Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2 Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tối ưu nhất.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong học tập.
Cho điểm O và đường thẳng (Delta ) không đi qua O.
Video hướng dẫn giải
Cho điểm O và đường thẳng \(\Delta \) không đi qua O. Gọi d là đường thẳng đi qua O và song song với \(\Delta \). Xét hai mặt phẳng phân biệt tuỳ ý (P) và (Q) cùng chứa d. Trong các mặt phẳng (P), (Q) tương ứng kẻ các đường thẳng a, b cùng đi qua O và vuông góc với d (H.7.16). Giải thích vì sao mp(a, b) đi qua O và vuông góc với \(\Delta \).
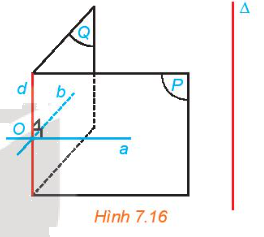
Phương pháp giải:
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
Lời giải chi tiết:
\(\left. \begin{array}{l}a \bot d\\d//\Delta \end{array} \right\} \Rightarrow \Delta \bot a\)
\(\left. \begin{array}{l}b \bot d\\d//\Delta \end{array} \right\} \Rightarrow \Delta \bot b\)
Mà \(a \cap b = \left\{ O \right\}\) \( \Rightarrow \) mp(a, b) đi qua O và vuông góc với \(\Delta \).
Video hướng dẫn giải
Cho mặt phẳng (P) và điểm O. Trong mặt phẳng (P), lấy hai đường thẳng cắt nhau a, b tuỳ ý. Gọi \(\left( \alpha \right),\left( \beta \right)\) là các mặt phẳng qua O và tương ứng vuông góc với a, b (H.7.19).

a) Giải thích vì sao hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) cắt nhau theo một đường thẳng \(\Delta \) đi qua O.
b) Nêu nhận xét về mối quan hệ giữa \(\Delta \) và (P).
Phương pháp giải:
- 2 mặt phẳng cắt nhau theo 1 giao tuyến là đường thẳng.
- Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
Lời giải chi tiết:
a) Vì \(\left( \alpha \right),\left( \beta \right)\) là các mặt phẳng qua O và giao 2 mặt phẳng là 1 đường thẳng nên hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) cắt nhau theo một đường thẳng đi qua O.
b) Gọi \(\Delta \) là giao tuyến của 2 \(\left( \alpha \right),\left( \beta \right)\)
\(\left. \begin{array}{l}a \bot \left( \alpha \right)\\\Delta \subset \left( \alpha \right)\end{array} \right\} \Rightarrow a \bot \Delta \)
\(\left. \begin{array}{l}b \bot \left( \beta \right)\\\Delta \subset \left( \beta \right)\end{array} \right\} \Rightarrow b \bot \Delta \)
Mà \(a \cap b = \left\{ I \right\} \Rightarrow \Delta \bot \left( P \right)\)
Video hướng dẫn giải
Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc với một mặt phẳng (P). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Phương pháp giải:
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng.
Lời giải chi tiết:
Vì AB và AC cùng vuông góc với một mặt phẳng (P) nên AB trùng AC
\( \Rightarrow \) A, B, C thẳng hàng.
Mục 2 của chương trình Toán 11 tập 2 Kết nối tri thức tập trung vào các kiến thức về phép biến hình. Cụ thể, trang 33 và 34 SGK đề cập đến việc tìm ảnh của một điểm, một đường thẳng, một đường tròn qua phép tịnh tiến, phép quay, và phép đối xứng trục.
Bài tập này yêu cầu học sinh xác định ảnh của các điểm, đường thẳng, đường tròn sau khi thực hiện phép tịnh tiến. Để giải quyết bài tập này, cần nắm vững định nghĩa và công thức của phép tịnh tiến. Ví dụ, nếu điểm M(x0, y0) tịnh tiến theo vectơ v = (a, b) thì ảnh M'(x', y') của M được tính bởi x' = x0 + a và y' = y0 + b.
Phép quay là một phép biến hình quan trọng trong hình học. Bài tập liên quan đến phép quay thường yêu cầu học sinh tìm ảnh của các điểm, đường thẳng, đường tròn sau khi thực hiện phép quay quanh một điểm cho trước với một góc quay nhất định. Công thức tính tọa độ điểm sau phép quay cần được ghi nhớ và áp dụng linh hoạt.
Phép đối xứng trục là phép biến hình biến mỗi điểm thành điểm đối xứng của nó qua một trục cho trước. Bài tập về phép đối xứng trục thường yêu cầu học sinh xác định ảnh của các điểm, đường thẳng, đường tròn sau khi thực hiện phép đối xứng trục. Nắm vững tính chất của đường trung trực của đoạn thẳng nối hai điểm đối xứng qua một trục là chìa khóa để giải quyết các bài tập này.
Ví dụ: Cho điểm A(1, 2) và vectơ tịnh tiến v = (3, -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vectơ v.
Giải: Áp dụng công thức phép tịnh tiến, ta có:
Vậy, A'(4, 1).
Khi giải các bài tập về phép biến hình, cần chú ý đến thứ tự thực hiện các phép biến hình. Nếu một đối tượng được thực hiện nhiều phép biến hình liên tiếp, cần thực hiện từng phép một theo đúng thứ tự để đảm bảo kết quả chính xác.
Giải mục 2 trang 33, 34 SGK Toán 11 tập 2 Kết nối tri thức đòi hỏi sự nắm vững kiến thức về các phép biến hình và khả năng áp dụng công thức một cách linh hoạt. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin giải quyết các bài tập và đạt kết quả tốt trong môn Toán.
| Phép biến hình | Công thức |
|---|---|
| Tịnh tiến | M'(x' , y') = M(x + a, y + b) |
| Quay | Công thức phức tạp hơn, tùy thuộc vào tâm quay và góc quay |
| Đối xứng trục | M'(x', y') là điểm đối xứng của M qua trục Δ |