Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 57, 58 SGK Toán 11 tập 2 chương trình Kết nối tri thức. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 11 và đạt kết quả cao trong học tập.
Cho hai đường thẳng chéo nhau a và b.
Video hướng dẫn giải
Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).
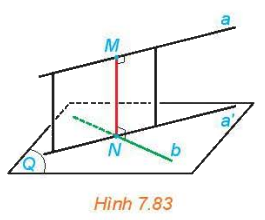
a) Mặt phẳng chứa a và a' có vuông góc với (Q) hay không?
b) Đường thẳng MN có vuông góc với cả hai đường thẳng a và b hay không?
c) Nêu mối quan hệ của khoảng cách giữa a, (Q) và độ dài đoạn thẳng MN.
Phương pháp giải:
Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P).
Lời giải chi tiết:
a) Mặt phẳng chứa a và a' có vuông góc với (Q)
b) Ta có \(MN \bot \left( Q \right),b \subset \left( Q \right) \Rightarrow MN \bot b\)
\(MN \bot a\) (M là hình chiếu của N trên a)
Vậy MN có vuông góc với cả hai đường thẳng a và b.
c) Vì a // (Q) nên d(a, (Q)) = d(M, (Q)) = MN
Video hướng dẫn giải
Cho đường thẳng a vuông góc với mặt phẳng (P) và cắt (P) tại O. Cho đường thẳng b thuộc mặt phẳng (P). Hãy tìm mối quan hệ giữa khoảng cách giữa a, b và khoảng cách từ O đến b (H.7.88).

Phương pháp giải:
Nếu đường vuông góc chung \(\Delta \) cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b.
Lời giải chi tiết:
Vì \(a \bot \left( P \right)\) tại O, \(OH \subset \left( P \right) \Rightarrow a \bot OH\)tại O
\(OH \bot b\) tại H
\( \Rightarrow d\left( {a,b} \right) = OH\)
Video hướng dẫn giải
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right),SA = a\sqrt 2 .\)
a) Tính khoảng cách từ A đến SC.
b) Chứng minh \(BD \bot \left( {SAC} \right).\)
c) Xác định đường vuông góc chung và tính khoảng cách giữa BD và SC.
Phương pháp giải:
- Khoảng cách từ một điểm M đến một đường thẳng a là khoảng cách giữa M và hình chiếu H của M trên a.
- Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng đó.
- Nếu đường vuông góc chung \(\Delta \) cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b.
Lời giải chi tiết:

a) Trong (SAC) kẻ \(AH \bot SC \Rightarrow d\left( {A,SC} \right) = AH\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
Xét ta giác SAC vuông tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} = \frac{1}{{{a^2}}} \Rightarrow AH = a\)
\( \Rightarrow d\left( {A,SC} \right) = a\)
b) Ta có \(BD \bot AC,BD \bot SA\left( {SA \bot \left( {ABCD} \right)} \right) \Rightarrow BD \bot \left( {SAC} \right)\)
c) Trong (SAC) kẻ \(OK \bot SC\)
\(\begin{array}{l}OK \bot BD\left( {BD \bot \left( {SAC} \right)} \right)\\ \Rightarrow d\left( {SC,BD} \right) = OK\end{array}\)
Xét tam giác AHC vuông tại H có
O là trung điểm AC
OK // AH (cùng vuông góc SC)
\( \Rightarrow \) OK là đường trung bình \( \Rightarrow \) \(OK = \frac{1}{2}AH = \frac{a}{2}\)\( \Rightarrow d\left( {BD,SC} \right) = \frac{a}{2}\)
Video hướng dẫn giải
Khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia. Hãy thảo luận để làm rõ nhận xét này.
Phương pháp giải:
Dựa vào lý thuyết về khoảng cách đã học của bài
Lời giải chi tiết:
- Khoảng cách từ một điểm M đến một đường thẳng a là khoảng cách giữa M và hình chiếu H của M trên a.
- Khoảng cách từ điểm M đến mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P)
- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P).
- Khoảng cách giữa hai mặt phẳng song song (P) và (Q) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.
Mà đường vuông góc là đường ngắn nhất nên khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia.
Mục 3 trong SGK Toán 11 tập 2 Kết nối tri thức tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Các bài tập trang 57 và 58 thường xoay quanh việc xác định vị trí tương đối giữa đường thẳng và mặt phẳng, tìm giao điểm, góc giữa chúng, và chứng minh các tính chất liên quan. Việc nắm vững các định lý, tính chất và phương pháp giải bài tập trong mục này là vô cùng quan trọng để xây dựng nền tảng vững chắc cho các kiến thức hình học không gian ở các lớp trên.
Bài tập này yêu cầu học sinh vận dụng các kiến thức về điều kiện để đường thẳng song song, cắt hoặc nằm trong mặt phẳng. Để giải quyết bài toán, cần xác định các yếu tố quan trọng như vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng. Việc kiểm tra tích vô hướng của các vectơ này sẽ giúp xác định mối quan hệ giữa đường thẳng và mặt phẳng.
Để tìm giao điểm của đường thẳng và mặt phẳng, ta cần giải hệ phương trình bao gồm phương trình tham số của đường thẳng và phương trình của mặt phẳng. Nghiệm của hệ phương trình chính là tọa độ của giao điểm. Nếu hệ phương trình vô nghiệm, đường thẳng song song với mặt phẳng hoặc không có điểm chung.
Ví dụ, cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): x + y + z - 6 = 0. Thay các phương trình tham số của d vào phương trình (P), ta được: (1 + t) + (2 - t) + (3 + 2t) - 6 = 0. Giải phương trình này, ta tìm được t = 0. Thay t = 0 vào phương trình tham số của d, ta được giao điểm I(1, 2, 3).
Góc giữa đường thẳng và mặt phẳng được tính bằng góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng. Để tính góc này, ta sử dụng công thức: sin(θ) = |cos(α)|, trong đó θ là góc giữa đường thẳng và mặt phẳng, α là góc giữa vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng.
Ví dụ, cho đường thẳng d có vectơ chỉ phương a = (1, 2, 3) và mặt phẳng (P) có vectơ pháp tuyến n = (4, 5, 6). Ta tính cos(α) = (a.n) / (||a|| * ||n||) = (1*4 + 2*5 + 3*6) / (√(1^2 + 2^2 + 3^2) * √(4^2 + 5^2 + 6^2)) = 32 / (√14 * √77). Từ đó, ta tính được sin(θ) = |cos(α)| và suy ra góc θ.
Học Toán 11 đòi hỏi sự kiên trì và luyện tập thường xuyên. Hãy dành thời gian ôn tập lý thuyết, làm bài tập và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Sử dụng các nguồn tài liệu học tập trực tuyến như giaitoan.edu.vn để bổ sung kiến thức và tìm hiểu các phương pháp giải bài tập hiệu quả.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập mục 3 trang 57, 58 SGK Toán 11 tập 2 Kết nối tri thức. Chúc các em học tập tốt!