Bài 4.2 trang 77 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài học này tập trung vào việc giải quyết các bài toán liên quan đến vectơ, đặc biệt là các phép toán vectơ và ứng dụng của chúng trong hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC). Lấy D, E là các điểm lần lượt thuộc các cạnh SA, SB và D, E khác S. a) Đường thẳng DE có nằm trong mặt phẳng (SAB) không? b) Giả sử DE cắt AB tại F. Chứng minh rằng F là điểm chung của hai mặt phẳng (SAB) và (CDE).
Đề bài
Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC). Lấy D, E là các điểm lần lượt thuộc các cạnh SA, SB và D, E khác S.
a) Đường thẳng DE có nằm trong mặt phẳng (SAB) không?
b) Giả sử DE cắt AB tại F. Chứng minh rằng F là điểm chung của hai mặt phẳng (SAB) và (CDE).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó.
Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.
Lời giải chi tiết
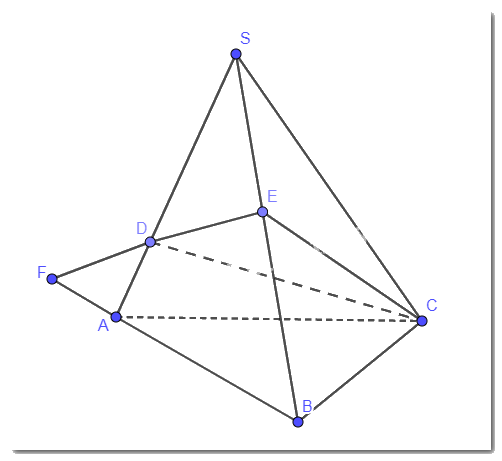
a) Ta có các điểm D, E đều nằm trong mp(SAB) nên đường thẳng DE nằm trong mp (SAB).
b) F thuộc AB suy ra F nằm trong mp (SAB).
F thuộc DE suy ra F nằm trong mp(CDE).
Do đó, F là điểm chung của hai mặt phẳng (SAB)và (CDE).
Bài 4.2 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng. Dưới đây là giải chi tiết bài tập này, cùng với hướng dẫn từng bước để bạn có thể tự giải và hiểu rõ hơn về phương pháp.
Bài tập yêu cầu chúng ta thực hiện các phép toán với vectơ, bao gồm cộng, trừ, nhân với một số thực, và tính độ dài của vectơ. Ngoài ra, bài tập còn yêu cầu chúng ta sử dụng vectơ để giải quyết các bài toán hình học, chẳng hạn như chứng minh hai đường thẳng song song, hoặc tìm tọa độ của một điểm.
Để giải bài tập này, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Dưới đây là giải chi tiết từng phần của bài tập 4.2 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức:
Giải:
Giải:
k.a = (3 * 2; 3 * -1) = (6; -3)
Giải:
a.b = (1 * 0) + (0 * 1) = 0
Giải:
Hai đường thẳng d1 và d2 song song khi và chỉ khi vectơ pháp tuyến của chúng cùng phương. Vectơ pháp tuyến của d1 là n1 = (1; 1), vectơ pháp tuyến của d2 là n2 = (1; 1). Vì n1 = n2, nên hai đường thẳng d1 và d2 song song.
Để củng cố kiến thức về vectơ và ứng dụng của chúng, bạn có thể luyện tập thêm các bài tập sau:
Bài 4.2 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng. Hy vọng với giải chi tiết và hướng dẫn từng bước trên đây, bạn đã hiểu rõ hơn về phương pháp giải bài tập này và có thể tự giải các bài tập tương tự một cách hiệu quả.
Chúc bạn học tốt!