Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2 Kết nối tri thức. Mục 3 trang 22, 23 tập trung vào các kiến thức quan trọng về đạo hàm, giúp học sinh nắm vững lý thuyết và kỹ năng giải bài tập.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập tốt nhất với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giải bài tập khoa học.
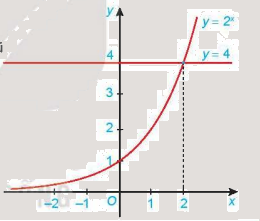
Cho đồ thị của hàm số (y = {2^x}) và (y = 4) như Hình 6.7.
Video hướng dẫn giải
Cho đồ thị của hàm số \(y = {2^x}\) và \(y = 4\) như Hình 6.7. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 và từ đó suy ra tập nghiệm của bất phương trình \({2^x} > 4.\)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 là \(\left( {2; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \({2^x} > 4\) là \(\left( {2; + \infty } \right)\)
Video hướng dẫn giải
Giải các bất phương trình sau:
a) \(0,{1^{2x - 1}} \le 0,{1^{2 - x}};\)
b) \({3.2^{x + 1}} \le 1.\)
Phương pháp giải:
Xét bất phương trình dạng \({a^x} > b\)
+) a > 1, nghiệm của bất phương trình là \(x > {\log _a}b\)
+) 0 < a < 1, nghiệm của bất phương trình là \(x < {\log _a}b\)
Lời giải chi tiết:
a) \(0,{1^{2x - 1}} \le 0,{1^{2 - x}} \Leftrightarrow 2x - 1 \ge 2 - x \Leftrightarrow 3x \ge 3 \Leftrightarrow x \ge 1\)
b) \({3.2^{x + 1}} \le 1 \Leftrightarrow {2^{x + 1}} \le \frac{1}{3} \Leftrightarrow x + 1 \le {\log _2}\frac{1}{3} \Leftrightarrow x \le - {\log _2}3 - 1 = - {\log _2}3 - {\log _2}2 = - {\log _2}6\)
Mục 3 trong SGK Toán 11 tập 2 Kết nối tri thức tập trung vào việc ứng dụng đạo hàm để khảo sát hàm số. Đây là một phần quan trọng trong chương trình học, giúp học sinh hiểu rõ hơn về tính chất của hàm số và cách sử dụng đạo hàm để tìm cực trị, khoảng đơn điệu, và điểm uốn. Việc nắm vững kiến thức này là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương sau.
Mục 3 bao gồm các nội dung chính sau:
a) Tìm tập xác định của hàm số:
Hàm số y = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là R.
b) Tính đạo hàm cấp nhất:
y' = 3x2 - 6x
c) Tìm điểm dừng:
Giải phương trình y' = 0, ta được:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy x = 0 hoặc x = 2
d) Lập bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
e) Kết luận:
Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 với giá trị y = 2, đạt cực tiểu tại x = 2 với giá trị y = -2.
(Tiếp tục giải chi tiết bài 2 tương tự như bài 1, bao gồm các bước tìm tập xác định, tính đạo hàm, tìm điểm dừng, lập bảng biến thiên và kết luận.)
Việc giải bài tập mục 3 trang 22, 23 SGK Toán 11 tập 2 Kết nối tri thức đòi hỏi sự hiểu biết vững chắc về đạo hàm và các ứng dụng của nó. Hy vọng với lời giải chi tiết và các mẹo học tập trên, bạn sẽ tự tin hơn trong việc chinh phục môn Toán.