Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 1 - Kết nối tri thức. Mục 4 trang 36 là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
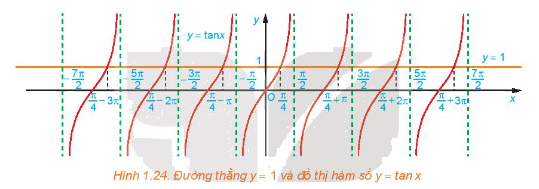
a) Quan sát Hình 1.24, hãy cho biết đường thẳng (y = 1) cắt đồ thị hàm số (y = tan x) tại mấy điểm trên khoảng (left( { - frac{pi }{2};frac{pi }{2}} right)?)
Video hướng dẫn giải
a) Quan sát Hình 1.24, hãy cho biết đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\) tại mấy điểm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)?\)
b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho
Phương pháp giải:
Nghiệm của phương trình \(\tan x = 1\) là hoành độ các giao điểm của đường thẳng \(y = 1\) và đồ thị hàm số \(y = \tan x\)
Lời giải chi tiết:
a) Từ Hình 1.24, ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\;\)tại 1 điểm \(x = \frac{\pi }{4}\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Video hướng dẫn giải
Giải các phương trình sau:
a) \(\sqrt 3 \tan 2x = - 1\); b) \(\tan 3x + \tan 5x = 0\)’
Phương pháp giải:
Dựa vào công thức nghiệm tổng quát: \(\tan x = m\; \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết:
a) \(\sqrt 3 \tan 2x = - 1\;\; \Leftrightarrow \tan 2x = - \frac{1}{{\sqrt 3 }}\;\;\; \Leftrightarrow \tan 2x = \tan - \frac{\pi }{6}\; \Leftrightarrow 2x = - \frac{\pi }{6} + k\pi \)
\(\;\; \Leftrightarrow x = - \frac{\pi }{{12}} + \frac{{k\pi }}{2}\;\left( {k \in \mathbb{Z}} \right)\)
b) \(\tan 3x + \tan 5x = 0\;\; \Leftrightarrow \tan 3x = \tan \left( { - 5x} \right) \Leftrightarrow 3x = - 5x + k\pi \;\; \Leftrightarrow 8x = k\pi \;\; \Leftrightarrow x = \frac{{k\pi }}{8}\;\left( {k \in \mathbb{Z}} \right)\)
Mục 4 trang 36 SGK Toán 11 tập 1 - Kết nối tri thức thường tập trung vào các bài toán liên quan đến phép biến hình, đặc biệt là phép tịnh tiến và phép quay. Để giải quyết các bài toán này một cách hiệu quả, học sinh cần nắm vững định nghĩa, tính chất của các phép biến hình và cách xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép biến hình.
Để giải các bài tập về phép biến hình, học sinh có thể áp dụng các phương pháp sau:
Ví dụ 1: Cho điểm A(1; 2). Tìm ảnh của điểm A qua phép tịnh tiến theo vectơ v = (3; -1).
Lời giải: Gọi A'(x'; y') là ảnh của điểm A qua phép tịnh tiến theo vectơ v. Ta có:
x' = 1 + 3 = 4
y' = 2 - 1 = 1
Vậy A'(4; 1).
Ví dụ 2: Cho điểm B(2; -3). Tìm ảnh của điểm B qua phép quay tâm O(0; 0) góc 90 độ.
Lời giải: Gọi B'(x'; y') là ảnh của điểm B qua phép quay tâm O(0; 0) góc 90 độ. Ta có:
x' = -(-3) = 3
y' = 2
Vậy B'(3; 2).
Để nắm vững kiến thức về phép biến hình, học sinh nên luyện tập thường xuyên các bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú và đa dạng, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải quyết vấn đề.
Giải mục 4 trang 36 SGK Toán 11 tập 1 - Kết nối tri thức đòi hỏi học sinh phải nắm vững lý thuyết, phương pháp giải và luyện tập thường xuyên. Hy vọng rằng với những hướng dẫn chi tiết và bài tập phong phú của giaitoan.edu.vn, bạn sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán.