Chào mừng bạn đến với bài học về Lý thuyết Lũy thừa với số mũ thực dành cho học sinh lớp 11 chương trình Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về lũy thừa, số mũ thực, cùng với các ví dụ minh họa dễ hiểu.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn trải nghiệm học toán online hiệu quả và thú vị.
1. Lũy thừa với số mũ nguyên
1. Lũy thừa với số mũ nguyên
a) Định nghĩa
- Cho n là một số nguyên dương. Ta định nghĩa:
Với a là số thực tùy ý:
\({a^n} = \underbrace {a.a.a...a}_{n\,thừa\,số}\)
Với a là số thực khác 0:
\({a^0} = 1;{a^{ - n}} = \frac{1}{{{a^n}}}\).
- Trong biểu thức \({a^m}\), a gọi là cơ số, m gọi là số mũ.
Chú ý: \({0^0}\) và \({0^{ - n}}\left( {n \in \mathbb{N}*} \right)\) không có nghĩa.
b) Tính chất
Với \(a \ne 0,b \ne 0\) và m, n là các số nguyên, ta có:
\(\begin{array}{l}{a^m}.{a^n} = {a^{m + n}};\\\frac{{{a^m}}}{{{a^n}}} = {a^{m - n}};\\{\left( {{a^m}} \right)^n} = {a^{mn}};\\{\left( {ab} \right)^m} = {a^m}.{b^m};\\{\left( {\frac{a}{b}} \right)^m} = \frac{{{a^m}}}{{{b^m}}}.\end{array}\)
Chú ý:
- Nếu \(a > 1\) thì \({a^m} > {a^n}\) khi và chỉ khi m > n.
- Nếu \(0 < a < 1\) thì \({a^m} > {a^n}\) khi và chỉ khi m < n.
2. Lũy thừa với số mũ hữu tỉ
a) Khái niệm căn bậc n
Cho số thực a và số nguyên dương n. Số b được gọi là căn bậc n của số a nếu \({b^n} = a\).
Nhận xét: Khi n là số lẻ, mỗi số thực a chỉ có một căn bậc n và kí hiệu là \(\sqrt[n]{a}\) (gọi là căn số học bậc n của a), giá trị âm kí hiệu là \( - \sqrt[n]{a}\).
Chú ý: \(\sqrt[n]{0} = 0\left( {n \in \mathbb{N}*} \right)\).
b) Tính chất của căn bậc n
Giả sử n, k là các số nguyên dương, m là số nguyên. Khi đó:
\(\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}\)
\(\frac{{\sqrt[n]{a}}}{{\sqrt[n]{b}}} = \sqrt[n]{{\frac{a}{b}}}\)
\({\left( {\sqrt[n]{a}} \right)^m} = \sqrt[n]{{{a^m}}}\)
\(\sqrt[n]{{\sqrt[k]{a}}} = \sqrt[{nk}]{a}\)
(Giả thiết các biểu thức ở trên đều có nghĩa).
c) Nhận biết lũy thừa với số mũ hữu tỉ
Cho số thực a và số hữu tỉ \(r = \frac{m}{n}\), trong đó m là một số nguyên và n là một số nguyên dương. Lũy thừa của a với số mũ r, kí hiệu là \({a^r}\), xác định bởi \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\).
Lưu ý: \({\left( {\sqrt[n]{a}} \right)^n} = a\).
Chú ý: Lũy thừa với số mũ hữu tỉ (của một số thực dương) có đầy đủ tính chất như lũy thừa với số mũ nguyên đã nêu trong Mục 1.
3. Lũy thừa với số mũ thực
Cho a là số thực dương và \(\alpha \) là một số vô tỉ. Xét dãy số hữu tỉ \(\left( {{r_n}} \right)\) mà \(\mathop {\lim }\limits_{n \to + \infty } {r_n} = \alpha \). Khi đó, dãy số \(\left( {{a^{{r_n}}}} \right)\) có giới hạn xác định và không phụ thuộc vào dãy số hữu tỉ \(\left( {{r_n}} \right)\) đã chọn. Giới hạn đó gọi là lũy thừa của a với số mũ \(\alpha \), kí hiệu là \({a^\alpha }\).
\({a^\alpha } = \mathop {\lim }\limits_{n \to + \infty } {a^{{r_n}}}\).
Chú ý: Lũy thừa với số mũ thực (của một số thực dương) có đầy đủ tính chất như lũy thừa với số mũ nguyên đã nêu trong Mục 1.
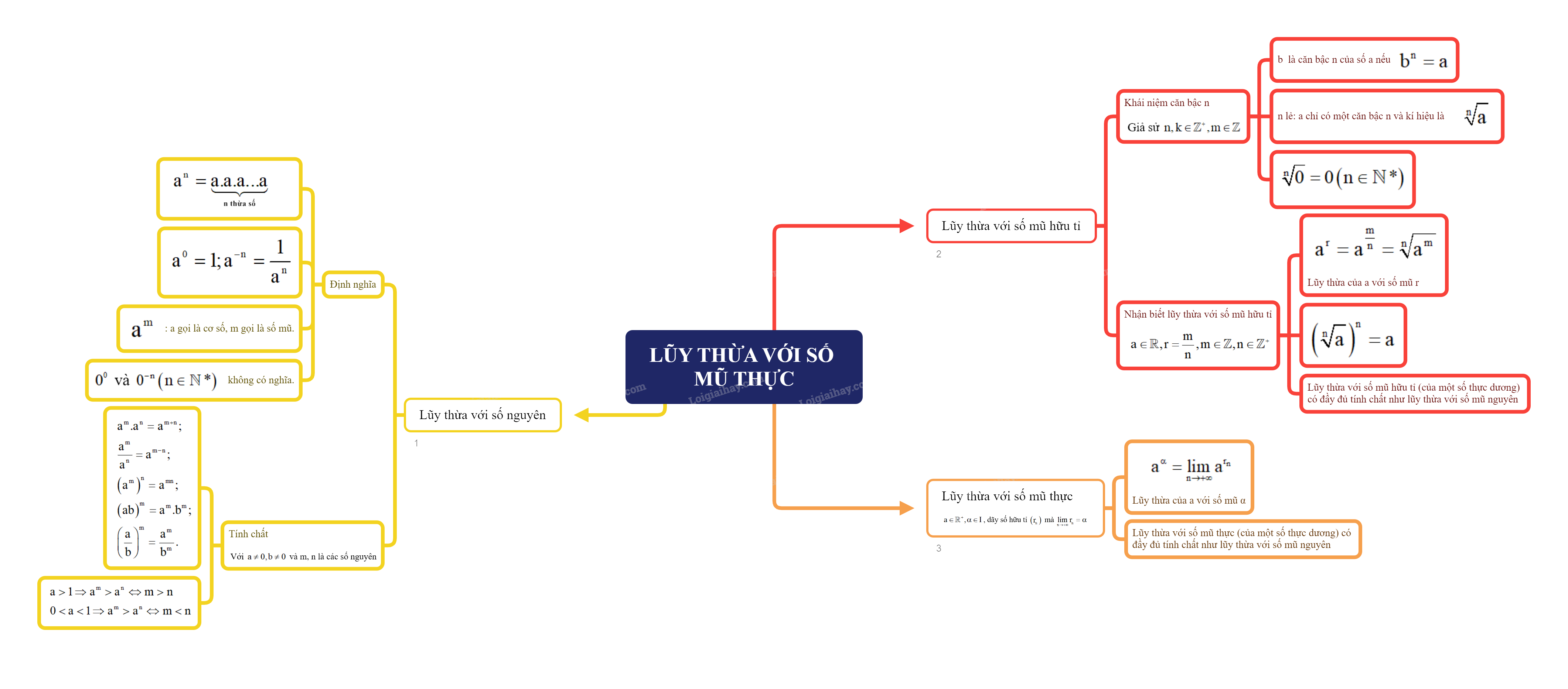
Lũy thừa với số mũ thực là một phần quan trọng trong chương trình Toán 11 Kết nối tri thức. Nó mở rộng khái niệm lũy thừa từ số mũ nguyên sang số mũ thực, cho phép chúng ta biểu diễn và tính toán các biểu thức phức tạp hơn. Bài viết này sẽ trình bày chi tiết về lý thuyết này, bao gồm định nghĩa, tính chất và các ứng dụng thực tế.
Với a là một số thực dương và α là một số thực bất kỳ, lũy thừa của a với số mũ α, ký hiệu là aα, là một số thực duy nhất được xác định bởi các tính chất sau:
Lưu ý rằng, nếu a = 0 thì lũy thừa 0α chỉ xác định khi α > 0.
Nếu n là một số nguyên dương, lũy thừa bậc n của a, ký hiệu là an, là tích của n thừa số bằng a:
an = a.a.a…a (n thừa số)
Đặc biệt:
Căn bậc n của một số thực a, ký hiệu là n√a, là một số x sao cho xn = a.
Ví dụ:
Lưu ý:
Có mối liên hệ mật thiết giữa lũy thừa và căn thức:
n√a = a1/n
Tổng quát:
am/n = n√am
Các tính chất của lũy thừa với số mũ thực tương tự như các tính chất của lũy thừa với số mũ nguyên, nhưng cần lưu ý một số điểm sau:
Lũy thừa với số mũ thực có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
Bài 1: Tính giá trị của biểu thức 82/3
Giải:82/3 = (81/3)2 = 22 = 4
Bài 2: Rút gọn biểu thức a2.a3/a4
Giải:a2.a3/a4 = a2+3/a4 = a5/a4 = a5-4 = a
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về Lý thuyết Lũy thừa với số mũ thực - Toán 11 Kết nối tri thức. Chúc bạn học tập tốt!