Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 6 trang 29, 30 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hàm số \(y = \cot x\) a) Xét tính chẵn, lẻ của hàm số
Cho hàm số \(y = \cot x\)
a) Xét tính chẵn, lẻ của hàm số
b) Hoàn thành bảng giá trị của hàm số \(y = \cot x\) trên khoảng\(\;\left( {0;\pi } \right)\).
\(x\) | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\frac{{3\pi }}{4}\) | \(\frac{{5\pi }}{6}\) |
\(y = \cot x\) | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm \(M\left( {x;\cot x} \right)\) với \(x \in \left( {0;\pi } \right)\) và nối lại ta được đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\).
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = \pi \), ta được đồ thị của hàm số \(y = \cot x\) như hình dưới đây.
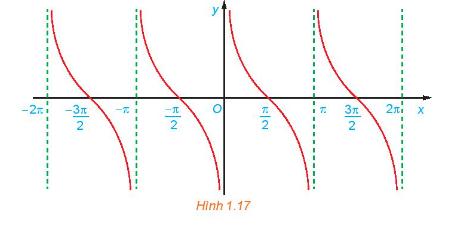
Từ đồ thị ở Hình 1.17, hãy tìm tập giá trị và các khoảng nghịch biến của hàm số \(y = \cot x\)
Phương pháp giải:
Sử dụng định nghĩa hàm số chẵn lẻ
Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cot \left( { - x} \right) = - \cot x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \cot x\) là hàm số lẻ.
b)
\(x\) | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\frac{{3\pi }}{4}\) | \(\frac{{5\pi }}{6}\) |
\(\cot x\) | \(\sqrt 3 \) | \(1\) | \(\frac{{\sqrt 3 }}{3}\) | \(0\) | \( - \frac{{\sqrt 3 }}{3}\) | \( - 1\) | \( - \sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \cot x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\).
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\) để hàm số \(y = \cot x\) nhận giá trị dương.
Phương pháp giải:
Nhìn đồ thị để xác định vị trí của y và x
Lời giải chi tiết:
Hàm số nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\), thì \(y > 0\) khi \(x\; \in \left( {0;\frac{\pi }{2}} \right) \cup \left( {\;\pi ;\frac{{3\pi }}{2}} \right)\)
Mục 6 trong SGK Toán 11 tập 1 Kết nối tri thức tập trung vào việc nghiên cứu về hàm số bậc hai. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học toán ở các lớp trên. Việc nắm vững các khái niệm, tính chất và phương pháp giải bài tập liên quan đến hàm số bậc hai là điều cần thiết để đạt kết quả tốt trong môn Toán.
Mục 6 bao gồm các nội dung chính sau:
Bài tập này yêu cầu học sinh xác định tập xác định của các hàm số bậc hai. Lưu ý rằng tập xác định của hàm số bậc hai là tập R (tập hợp tất cả các số thực).
Bài tập này yêu cầu học sinh xác định hệ số a, b, c của hàm số bậc hai. Học sinh cần chú ý đến dạng tổng quát của hàm số bậc hai y = ax2 + bx + c.
Đỉnh của parabol có tọa độ (x0; y0), trong đó x0 = -b/2a và y0 = f(x0). Học sinh cần áp dụng công thức này để tìm tọa độ đỉnh của parabol.
Giao điểm của parabol với trục hoành là nghiệm của phương trình bậc hai ax2 + bx + c = 0. Học sinh cần sử dụng các phương pháp giải phương trình bậc hai để tìm nghiệm.
Giao điểm của parabol với trục tung là điểm có hoành độ x = 0. Học sinh cần thay x = 0 vào phương trình hàm số để tìm tung độ y.
Hàm số bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập hiệu quả được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài tập liên quan đến hàm số bậc hai. Chúc các em học tốt!