Lý thuyết Lôgarit - Toán 11 Kết nối tri thức

Chào mừng bạn đến với bài học về Lý thuyết Lôgarit trong chương trình Toán 11 Kết nối tri thức tại giaitoan.edu.vn. Bài viết này sẽ cung cấp một cách hệ thống và dễ hiểu về các khái niệm cơ bản, tính chất và ứng dụng của lôgarit.

Chúng tôi cam kết mang đến cho bạn những kiến thức toán học chất lượng, giúp bạn tự tin hơn trong học tập và thi cử.

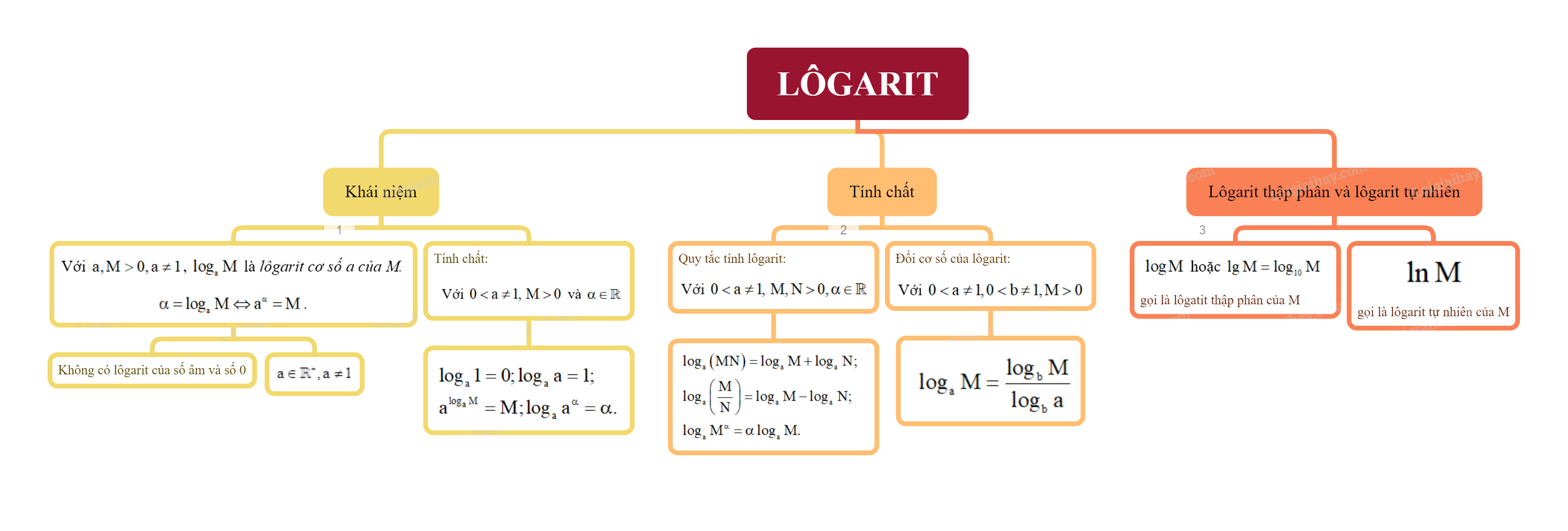
1. Khái niệm Lôgarit

1. Khái niệm Lôgarit

Cho a là một số thực dương khác 1 và M là một số thực dương. Số thực \(\alpha \) để \({a^\alpha } = M\) được gọi là lôgarit cơ số a của M và kí hiệu là \({\log _a}M\).

\(\alpha = {\log _a}M \Leftrightarrow {a^\alpha } = M\).

Chú ý: Không có lôgarit của số âm và số 0. Cơ số của lôgarit phải dương và khác 1. Từ định nghĩa lôgarit, ta có các tính chất sau:

Với \(0 < a \ne 1,\,\,M > 0\) và \(\alpha \) là số thực tùy ý, ta có:

\(\begin{array}{l}{\log _a}1 = 0;{\log _a}a = 1;\\{a^{{{\log }_a}M}} = M;{\log _a}{a^\alpha } = \alpha .\end{array}\)

2. Tính chất của lôgarit

a) Quy tắc tính lôgarit

Giả sử a là số thực dương khác 1, M và N là các số thực dương, \(\alpha \) là số thực tùy ý. Khi đó:

\(\begin{array}{l}{\log _a}\left( {MN} \right) = {\log _a}M + {\log _a}N;\\{\log _a}\left( {\frac{M}{N}} \right) = {\log _a}M - {\log _a}N;\\{\log _a}{M^\alpha } = \alpha {\log _a}M.\end{array}\)

b) Đổi cơ số của lôgarit

Với các cơ số lôgarit a và b bất kì (\(0 < a \ne 1,0 < b \ne 1\)) và M là số thực dương tùy ý, ta luôn có:

\({\log _a}M = \frac{{{{\log }_b}M}}{{{{\log }_b}a}}\).

3. Lôgarit thập phân và lôgarit tự nhiên

a) Lôgarit thập phân

Lôgarit cơ số 10 của một số dương M gọi là lôgatit thập phân của M, kí hiệu là \(\log M\) hoặc \(\lg M\) (đọc là lốc của M).

b) Số e và lôgarit tự nhiên

Lôgarit cơ số e của một số dương M gọi là lôgarit tự nhiên của M, kí hiệu là \(\ln M\) (đọc là lôgarit Nêpe của M).

Lý thuyết Lôgarit - Toán 11 Kết nối tri thức 1

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Lý thuyết Lôgarit - Toán 11 Kết nối tri thức – hành trang không thể thiếu trong chuyên mục Sách bài tập Toán 11 trên nền tảng soạn toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Lý thuyết Lôgarit - Toán 11 Kết nối tri thức

Lôgarit là một khái niệm quan trọng trong toán học, đặc biệt là trong chương trình Toán 11 Kết nối tri thức. Nó đóng vai trò then chốt trong việc giải quyết nhiều bài toán về phương trình, bất phương trình mũ và các bài toán thực tế khác.

1. Định nghĩa Lôgarit

Lôgarit của một số dương b (với b ≠ 1) với cơ số a dương (a ≠ 1) là số x sao cho a^x = b. Ký hiệu: x = log_ab.

a là cơ số của lôgarit.
b là số bị lôgarit (còn gọi là đối số).
x là giá trị của lôgarit.

2. Điều kiện tồn tại của Lôgarit

Lôgarit log_ab tồn tại khi và chỉ khi a > 0, a ≠ 1 và b > 0.

3. Các Tính chất Cơ bản của Lôgarit

log_a1 = 0 (với a > 0, a ≠ 1)
log_aa = 1 (với a > 0, a ≠ 1)
log_a(xy) = log_ax + log_ay (với x > 0, y > 0, a > 0, a ≠ 1)
log_a(x/y) = log_ax - log_ay (với x > 0, y > 0, a > 0, a ≠ 1)
log_axⁿ = n log_ax (với x > 0, a > 0, a ≠ 1)
log_ab = 1/log_ba (với a > 0, a ≠ 1, b > 0, b ≠ 1)

4. Đổi Cơ Số Lôgarit

Công thức đổi cơ số lôgarit: log_ab = log_cb / log_ca (với a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1)

5. Lôgarit Cơ Số 10 và Lôgarit Tự Nhiên

Lôgarit cơ số 10 được ký hiệu là log x (thường dùng trong tính toán). Lôgarit tự nhiên (cơ số e) được ký hiệu là ln x (thường dùng trong các bài toán liên quan đến tăng trưởng, suy giảm).

6. Ứng dụng của Lôgarit

Giải phương trình mũ: Sử dụng tính chất biến đổi lôgarit để đưa phương trình về dạng đơn giản hơn.
Giải bất phương trình mũ: Tương tự như phương trình mũ, sử dụng tính chất biến đổi lôgarit để giải bất phương trình.
Tính toán các đại lượng trong các bài toán thực tế: Ví dụ, tính độ pH trong hóa học, tính cường độ âm thanh trong vật lý.

7. Ví dụ minh họa

Ví dụ 1: Tính log₂8.

Giải: Vì 2³ = 8 nên log₂8 = 3.

Ví dụ 2: Rút gọn biểu thức log₃9 + log₃27.

Giải: log₃9 + log₃27 = log₃(9 * 27) = log₃243 = 5.

8. Bài tập luyện tập

Để củng cố kiến thức về lý thuyết lôgarit, bạn có thể thực hành các bài tập sau:

Tính các giá trị của lôgarit: log₅25, log₁₀1000, log₂(1/4).
Rút gọn các biểu thức: log₂4 + log₂8, log₃81 - log₃9.
Giải các phương trình: log₂x = 3, log₃(x+1) = 2.

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết lôgarit trong chương trình Toán 11 Kết nối tri thức. Chúc bạn học tập tốt!