Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2 Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tối ưu nhất.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong học tập.
Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O'
Video hướng dẫn giải
Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a', b' tương ứng song song với m, n (H.7.2).
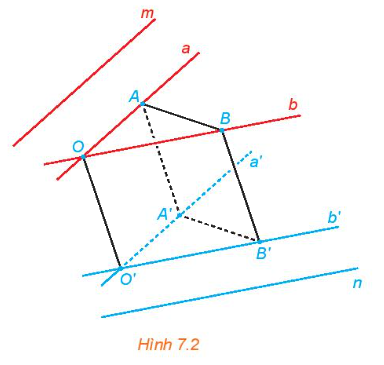
a) Mỗi cặp đường thẳng a, a và b, b' có cùng thuộc một mặt phẳng hay không?
b) Lấy các điểm A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO' cắt a' tại A', đường thẳng qua B song song với OO' cắt b' tại B' Giải thích vì sao OAA'O', OBB'O', ABB'A' là các hình bình hành.
c) So sánh góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b'.
(Gợi ý: Áp dụng định lí côsin cho các tam giác OAB, O'A'B').
Phương pháp giải:
- Tứ giác có các cặp cạnh đối song song là hình bình hành.
- Định lí côsin \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2ab}}\)
Lời giải chi tiết:
a) Mỗi cặp đường thẳng a, a' và b, b' cùng thuộc một mặt phẳng vì a // a', b // b'.
b) Ta có:
+) OA // O′A′; OO' // AA' nên OAA'O' là hình bình hành.
+) OB // O′B′; OO' // BB' nên OBB'O' là hình bình hành.
+) AB // A′B′ và OO' // AA'; OO' // BB' suy ra AA' // BB' nên ABB'A' là hình bình hành.
c) Áp dụng định lí côsin cho các tam giác OAB và O'A'B', ta có:
\(\cos \left( {a,b} \right) = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}};\cos \left( {a',b'} \right) = \frac{{O'{{A'}^2} + O'{{B'}^2} - A'{{B'}^2}}}{{2.O'A'.O'B'}}\)
Vì O'A' = OA và O'B' = OB; AB = A'B' nên cos(a,b) = cos(a′,b′).
Video hướng dẫn giải
Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) và (a', b') có mối quan hệ gì?
Phương pháp giải:
Sử dụng Hoạt động 1 trang 28
Lời giải chi tiết:
Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) = (a', b')
Video hướng dẫn giải
Kim tự tháp Cheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ thứ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Kim tự tháp có dạng hình chóp với đáy là hình vuông có cạnh dài khoảng 230 m, các cạnh bên bằng nhau và dài khoảng 219 m (kích thước hiện nay). (Theo britannica.com).

Tính (gần đúng) góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp (H.7.4).
Phương pháp giải:
Để xác định góc giữa hai đường thẳng chéo nhau a và b, ta có thể lấy một điểm O thuộc đường thẳng a và qua đó kẻ đường thẳng b' song song với b. Khi đó (a, b) = (a', b')
Lời giải chi tiết:
Vì AB // CD (ABCD là hình vuông) nên (SC, AB) = (SC, CD)
Xét tam giác SCD có
\(\cos \widehat {SCD} = \frac{{S{C^2} + C{D^2} - S{D^2}}}{{2SC.CD}} = \frac{{{{219}^2} + {{230}^2} - {{219}^2}}}{{2.219.230}} = \frac{{115}}{{219}} \Rightarrow \widehat {SCD} \approx 58,{32^0}\)
Vậy góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp bằng khoảng 58,320.
Mục 1 của chương trình Toán 11 tập 2 Kết nối tri thức tập trung vào các kiến thức về phép biến hình. Cụ thể, học sinh sẽ được làm quen với các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để hiểu sâu hơn về hình học không gian và các ứng dụng của nó.
Bài tập mục 1 trang 28, 29 SGK Toán 11 tập 2 Kết nối tri thức bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng kiến thức về các phép biến hình để giải quyết các vấn đề cụ thể. Các bài tập này thường xoay quanh việc xác định ảnh của một điểm, một đường thẳng hoặc một hình qua một phép biến hình nhất định. Ngoài ra, học sinh cũng cần phải chứng minh các tính chất liên quan đến các phép biến hình.
Để giúp học sinh giải quyết các bài tập một cách hiệu quả, giaitoan.edu.vn cung cấp lời giải chi tiết cho từng bài tập trong mục 1 trang 28, 29 SGK Toán 11 tập 2 Kết nối tri thức. Lời giải của chúng tôi không chỉ cung cấp đáp án đúng mà còn giải thích rõ ràng các bước thực hiện, giúp học sinh hiểu được bản chất của vấn đề và tự tin áp dụng kiến thức vào các bài tập tương tự.
Bài tập 1 yêu cầu học sinh xác định ảnh của điểm A(x0, y0) qua phép tịnh tiến theo vectơ v = (a, b). Để giải bài tập này, học sinh cần áp dụng công thức: A'(x0 + a, y0 + b). Ví dụ, nếu A(1, 2) và v = (3, -1) thì A'(1 + 3, 2 - 1) = A'(4, 1).
Bài tập 2 yêu cầu học sinh xác định ảnh của điểm B(x0, y0) qua phép quay tâm O(0, 0) góc α. Để giải bài tập này, học sinh cần áp dụng công thức: B'(x0cosα - y0sinα, x0sinα + y0cosα). Lưu ý rằng góc α phải được tính bằng radian.
Bài tập 3 yêu cầu học sinh xác định ảnh của điểm C(x0, y0) qua phép đối xứng trục d: y = x. Để giải bài tập này, học sinh cần đổi chỗ x và y: C'(y0, x0). Tương tự, nếu d: x = a thì C'(2a - x0, y0).
Bài tập 4 yêu cầu học sinh xác định ảnh của điểm D(x0, y0) qua phép đối xứng tâm I(a, b). Để giải bài tập này, học sinh cần áp dụng công thức: D'(2a - x0, 2b - y0).
Các phép biến hình có rất nhiều ứng dụng trong thực tế, đặc biệt trong lĩnh vực thiết kế đồ họa, kỹ thuật và khoa học. Ví dụ, phép tịnh tiến được sử dụng để di chuyển các đối tượng trên màn hình, phép quay được sử dụng để xoay các đối tượng, phép đối xứng được sử dụng để tạo ra các hình ảnh đối xứng. Việc hiểu rõ các phép biến hình sẽ giúp bạn có thể ứng dụng chúng vào các bài toán thực tế một cách hiệu quả.
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể của giaitoan.edu.vn, bạn sẽ tự tin giải quyết các bài tập trong mục 1 trang 28, 29 SGK Toán 11 tập 2 Kết nối tri thức. Chúc bạn học tập tốt!