Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2, sách Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài toán phức tạp.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài tập và đạt kết quả tốt nhất trong môn Toán.
Khi mua máy điều hoà, bác An được hướng dẫn rằng mỗi mét khối của phòng cần công suất điều hoà khoảng 200 BTU.
Video hướng dẫn giải
Khi mua máy điều hoà, bác An được hướng dẫn rằng mỗi mét khối của phòng cần công suất điều hoà khoảng 200 BTU. Căn phòng bác An cần lắp máy có dạng hình hộp chữ nhật, rộng 4 m, dài 5 m và cao 3 m. Hỏi bác An cần mua loại điều hoà có công suất bao nhiêu BTU?

Phương pháp giải:
Thể tích hình hộp chữ nhật = chiều dài x chiều rộng x chiều cao.
Lời giải chi tiết:
Thể tích của căn phòng là: \(V = 4.5.3 = 60\left( {{m^3}} \right)\).
Vì mỗi mét khối của phòng cần công suất điều hoà khoảng 200 BTU nên công suất cần thiết cho máy điều hoà của căn phòng bác An là: 60.200 = 12000 BTU.
Do đó, bác An cần mua một máy điều hoà có công suất khoảng 12 000 BTU để làm mát cho căn phòng của mình.
Video hướng dẫn giải
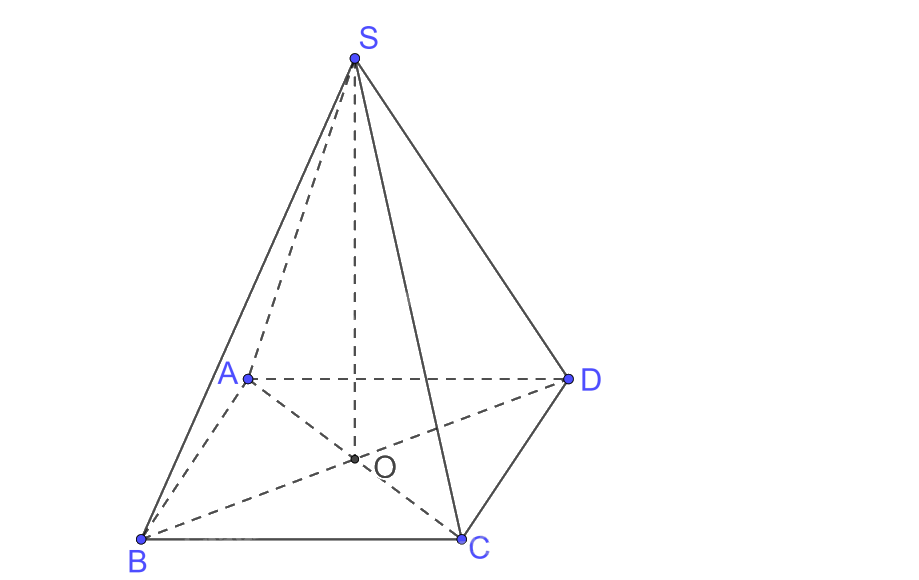
Cho khối chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích của khối chóp.

Phương pháp giải:
Thế tích khối chóp \(V = \frac{1}{3}h.S\)
Lời giải chi tiết:
Gọi \(AC \cap BD = \left\{ O \right\}\) mà S.ABCD là chóp đều nên \(SO \bot \left( {ABCD} \right)\).
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \).
\( \Rightarrow OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\).
Xét tam giác SAO vuông tại O có:
\(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{2}} = \frac{{\sqrt {4{b^2} - 2{a^2}} }}{2}\).
\({S_{ABCD}} = {a^2}\).
Vậy khối chóp có thể tích \(V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.\frac{{\sqrt {4{b^2} - 2{a^2}} }}{2}.{a^2} = \frac{{{a^2}\sqrt {4{b^2} - 2{a^2}} }}{6}\).
Video hướng dẫn giải
Cho khối chóp cụt đều ABC.A'B'C' có đường cao HH' = h, hai mặt đáy ABC, A'B'C' có cạnh tương ứng bằng 2a, a.
a) Tính thể tích của khối chóp cụt.
b) Gọi B1,C1 tương ứng là trung điểm của AB, AC. Chứng minh rằng AB1C1.A'B'C' là một hình lăng trụ. Tính thể tích khối lăng trụ AB1C1.A'B'C'.

Phương pháp giải:
Thể tích khối chóp cụt đều \(V = \frac{1}{3}.h.\left( {S + S' + \sqrt {S.S'} } \right)\).
Thể tích khối lăng trụ \(V = h.S\).
Lời giải chi tiết:
a) Tam giác đều ABC có diện tích \(S = \frac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \).
Tam giác đều A'B'C' có diện tích \(S' = \frac{{{a^2}\sqrt 3 }}{4}\).
Thể tích khối chóp cụt:
\(V = \frac{1}{3}.HH'.\left( {S + S' + \sqrt {S.S'} } \right) = \frac{1}{3}.h.\left( {{a^2}\sqrt 3 + \frac{{{a^2}\sqrt 3 }}{4} + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} } \right) = \frac{{7{a^2}\sqrt 3 }}{{12}}\).
b) Vì ABC.A'B'C' là khối chóp cụt đều nên (ABC) // (A'B'C').
Mà \(\left( {A{B_1}{C_1}} \right) \subset \left( {ABC} \right) \Rightarrow \left( {A{B_1}{C_1}} \right)//\left( {A'B'C'} \right)\).
Xét tam giác ABC có:
B1,C1 tương ứng là trung điểm của AB, AC.
\( \Rightarrow \) B1C1 là đường trung bình của tam giác ABC.
\( \Rightarrow \) \({B_1}{C_1} = \frac{{BC}}{2}\) và B1C1 // BC mà \(B'C' = \frac{{BC}}{2}\) và BC // B’C’.
\( \Rightarrow \) B1C1 = B’C’ và B1C1 // B’C’ \( \Rightarrow \) C1C’B’B1 là hình bình hành.
Ta có \(A{B_1} = A'B' = \frac{{AB}}{2},A{B_1}//A'B'\) \( \Rightarrow \) AA’B’B1 là hình bình hành.
\(A{C_1} = A'C' = \frac{{AC}}{2},A{C_1}//A'C'\) \( \Rightarrow \) AA’C’C1 là hình bình hành.
Do đó AB1C1.A'B'C' là một hình lăng trụ.
Thể tích hình lăng trụ \(V = HH'.S' = h.\frac{{{a^2}\sqrt 3 }}{4}\).
Video hướng dẫn giải
Một sọt đựng đồ có dạng hình chóp cụt đều (H.7.98). Đáy và miệng sọt là các hình vuông tương ứng có cạnh bằng 30 cm, 60 cm, cạnh bên của sọt dài 50 cm. Tính thể tích của sọt.

Phương pháp giải:
Thể tích khối chóp cụt đều \(V = \frac{1}{3}.h.\left( {S + S' + \sqrt {S.S'} } \right)\).
Lời giải chi tiết:
Đặt tên các điểm như hình vẽ, H là hình chiếu vuông góc của D’ lên mặt phẳng (ABCD).
Khi đó AB = 60, A’B’ = 30, DD’ = 50.
Áp dụng công thức tính đường chéo hình vuông, ta có \(BD = 60\sqrt 2 \), \(B'D' = 30\sqrt 2 \).
\(DH = \frac{{BD - B'D'}}{2} = \frac{{60\sqrt 2 {\rm{\;}} - 30\sqrt 2 }}{2} = 15\sqrt 2 \).
Chiều cao sọt là \(h = D'H = \sqrt {D'{D^2} - D'{H^2}} {\rm{\;}} = \sqrt {{{50}^2} - {{\left( {15\sqrt 2 } \right)}^2}} {\rm{\;}} = 5\sqrt {82} \).
Thể tích sọt có dạng khối chóp cụt đều là:
\(V = \frac{1}{3}h\left( {{S_1}^2 + \sqrt {{S_1}{S_2}} + {S_2}^2} \right) = \frac{1}{3}5\sqrt {82} \left( {{{60}^2} + \sqrt {{{60}^2}{{.30}^2}} + {{30}^2}} \right) \approx 95082\) \(\left( {c{m^3}} \right)\).
Chương trình Toán 11 tập 2, sách Kết nối tri thức, tập trung vào các chủ đề quan trọng như hàm số lượng giác, phương trình lượng giác, và các ứng dụng của lượng giác trong thực tế. Trang 61, 62, và 63 của sách chứa các bài tập rèn luyện kỹ năng giải quyết các vấn đề liên quan đến các kiến thức này. Việc nắm vững các khái niệm và phương pháp giải là chìa khóa để thành công trong môn Toán.
Các bài tập trên trang 61 thường tập trung vào việc vận dụng các công thức lượng giác cơ bản để tính toán giá trị của các biểu thức lượng giác. Ví dụ, các bài tập có thể yêu cầu tính sin, cos, tan, cot của các góc đặc biệt, hoặc rút gọn các biểu thức lượng giác phức tạp. Để giải quyết các bài tập này, bạn cần nắm vững các công thức lượng giác cơ bản và kỹ năng biến đổi đại số.
Trang 62 thường chứa các bài tập liên quan đến việc giải phương trình lượng giác. Các phương trình lượng giác có thể là phương trình lượng giác cơ bản, hoặc phương trình lượng giác phức tạp hơn. Để giải quyết các bài tập này, bạn cần nắm vững các phương pháp giải phương trình lượng giác, như phương pháp đặt ẩn phụ, phương pháp sử dụng công thức biến đổi lượng giác, và phương pháp sử dụng đường tròn lượng giác.
Các bài tập trên trang 63 thường tập trung vào việc ứng dụng kiến thức lượng giác vào giải quyết các bài toán thực tế. Ví dụ, các bài tập có thể yêu cầu tính chiều cao của một tòa nhà, khoảng cách giữa hai điểm, hoặc góc tạo bởi hai đường thẳng. Để giải quyết các bài tập này, bạn cần nắm vững các khái niệm về tam giác vuông, tam giác bất kỳ, và các công thức lượng giác liên quan.
Bài tập: Giải phương trình lượng giác: sin(x) = 1/2
Lời giải:
Việc giải các bài tập trang 61, 62, 63 SGK Toán 11 tập 2 - Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng rằng với những hướng dẫn và lời khuyên trên, bạn sẽ tự tin giải quyết các bài tập và đạt kết quả tốt nhất. Chúc bạn học tập tốt!