Chào mừng bạn đến với bài học về Lý thuyết Hai mặt phẳng song song, một phần quan trọng trong chương trình Hình học không gian lớp 11 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản, định nghĩa, tính chất và các dấu hiệu nhận biết hai mặt phẳng song song.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và đầy đủ, giúp bạn tự tin chinh phục môn Toán.
1. Hai mặt phẳng song song
1. Hai mặt phẳng song song
Hai mặt \(\left( \alpha \right)\) và \(\left( \beta \right)\) được gọi là song song với nhau nếu chúng không có điểm chung. Kí hiệu \(\left( \alpha \right)\)// \(\left( \beta \right)\) hay \(\left( \beta \right)\)//\(\left( \alpha \right)\).
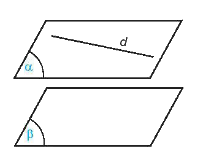
*Nhận xét: \(\left\{ \begin{array}{l}\left( \alpha \right)//\left( \beta \right)\\d \subset \left( \alpha \right)\end{array} \right. \Rightarrow d//\left( \beta \right)\).
2. Điều kiện và tính chất của hai mặt phẳng song song
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng phẳng \(\left( \beta \right)\)thì \(\left( \alpha \right)\)và \(\left( \beta \right)\)song song với nhau.
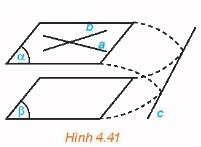
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
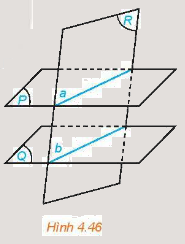
3. Định lí Thalès trong không gian
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.
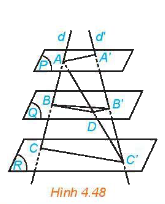
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\)
4. Hình lăng trụ và hình hộp
Cho hai mặt phẳng song song \(\left( \alpha \right)\) và \(\left( {\alpha '} \right)\). Trên \(\left( \alpha \right)\) cho đa thức đa giác lồi \({A_1}{A_2}...{A_n}\). Qua các đỉnh\({A_1},{A_2},...,{A_n}\)vẽ các đường thẳng đôi một song song và cắt mặt phẳng \(\left( {\alpha '} \right)\)tại \({A_1}',{A_2}',...,{A_n}'\). Hình gồm hai đa giác\({A_1}{A_2}...{A_n}\), \({A_1}'{A_2}'...{A_n}'\) và các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\)được gọi là hình lăng trụ và kí hiệu là \({A_1}{A_2}...{A_n}.{A_1}'{A_2}'...{A_n}'\).
Các điểm \({A_1},{A_2},...,{A_n}\) và \({A_1}',{A_2}',...,{A_n}'\)được gọi là các đỉnh, các đoạn thẳng \({A_1}{A_1}',{A_2}{A_2}',...,{A_n}{A_n}'\)được gọi là các cạnh bên, các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_n}{A_1}\)và \({A_1}'{A_2}',{A_2}'{A_3}',...,{A_n}'{A_1}'\) gọi là cạnh đáy của hình trụ.
Hai đa giác \({A_1}{A_2}...{A_n}\)và \({A_1}'{A_2}'...{A_n}'\)được gọi là hai mặt đáy của hình lăng trụ.
Các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\) gọi là các mặt bên của hình trụ.
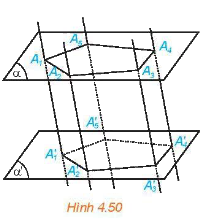
Hình lăng trụ tứ giác ABCD.A’B’C’D’ có hai đáy là hình bình hành được gọi là hình hộp.
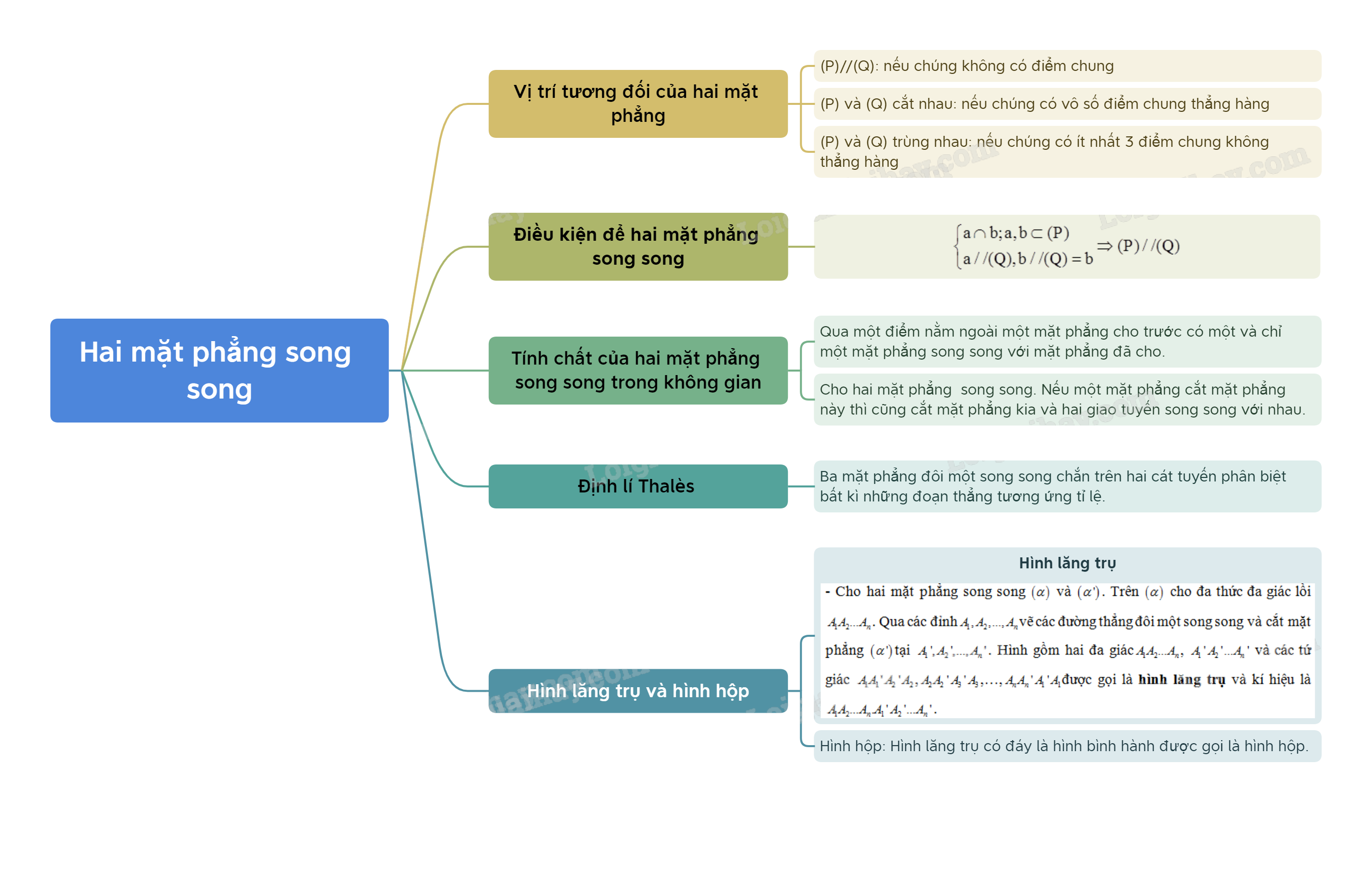
Trong chương trình Hình học không gian lớp 11, kiến thức về hai mặt phẳng song song đóng vai trò then chốt. Việc nắm vững lý thuyết này không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao hơn.
Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung. Ký hiệu: (P) // (Q). Điều này có nghĩa là khi kéo dài vô hạn, hai mặt phẳng này sẽ không giao nhau tại bất kỳ điểm nào.
Có một số điều kiện để xác định hai mặt phẳng song song:
Hai mặt phẳng song song có những tính chất quan trọng sau:
Để nhận biết hai mặt phẳng song song, ta có thể sử dụng các dấu hiệu sau:
Ví dụ 1: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh AB. Mặt phẳng (SMC) song song với mặt phẳng (ABD). Chứng minh rằng SC // AD.
Giải: Vì (SMC) // (ABD) và M là trung điểm của AB, nên giao điểm của SC và (ABD) là trung điểm của BD. Do đó, SC // AD.
Bài 1: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng (ABCD) // (A'B'C'D').
Bài 2: Cho hai mặt phẳng (P) và (Q) song song với nhau. Trên (P) có điểm A và trên (Q) có điểm B. Tìm quỹ tích của trung điểm I của đoạn AB.
Lý thuyết về hai mặt phẳng song song có ứng dụng rộng rãi trong thực tế, ví dụ như trong kiến trúc, xây dựng, thiết kế đồ họa,... Việc hiểu rõ lý thuyết này giúp chúng ta giải quyết các vấn đề liên quan đến không gian và hình học một cách hiệu quả.
Để nắm vững kiến thức về hai mặt phẳng song song, bạn nên luyện tập thêm nhiều bài tập khác nhau. Hãy tìm kiếm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Bài học về Lý thuyết Hai mặt phẳng song song đã cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất. Hãy ôn tập lại lý thuyết và luyện tập thêm để tự tin hơn trong các bài kiểm tra và kỳ thi sắp tới.
Chúc bạn học tốt!