Bài 3.7 trang 67 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Phỏng vấn một học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối, thu được bảng số liệu ở bên a) So sánh thời gian ngủ trung bình của các bạn học sinh nam và nữ b) Hãy cho biết 75% học sinh khối 11 ngủ ít nhất bao nhiêu giờ?
Đề bài
Phỏng vấn một học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối, thu được bảng số liệu ở bên
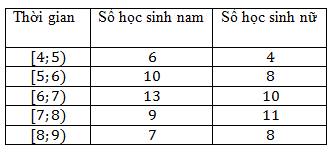
a) So sánh thời gian ngủ trung bình của các bạn học sinh nam và nữ.
b) Hãy cho biết 75% học sinh khối 11 ngủ ít nhất bao nhiêu giờ?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng công thức số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\)
\(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\)
trong đó \(n = {m_1} + \ldots + {m_k}\) là cỡ mẫu và là giá trị đại diện của nhóm \(\left[ {{a_i},{a_{i + 1}}} \right)\)
Để tính tứ phân vị thứ nhất\({Q_1}\)của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_1}\), giả sử đó là nhóm thứ \(p:\left[ {{a_p};\;{a_{p + 1}}} \right).\;\)Khi đó,
\({Q_1} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right)\),
Trong đó, n là cỡ mẫu, \({m_p}\) là tần số nhóm p, với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\).
Để tính tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_3}\). Giả sử đó là nhóm thứ \(p:\left[ {{a_p};\;{a_{p + 1}}} \right)\). Khi đó,
\({Q_3} = {a_p} + \frac{{\frac{{3n}}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right)\).
trong đó, n là cỡ mẫu, \({m_p}\) là tần số nhóm p, với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\).
Lời giải chi tiết
a)

Thời gian ngủ trung bình của các bạn nam
\({\bar x_{nam}} = \frac{{4.5 \times 6 + 5.5 \times 10 + 6.5 \times 13 + 7.5 \times 9 + 8.5 \times 7}}{{6 + 10 + 13 + 9 + 7}} = 6.52\).
Thời gian ngủ trung bình của các bạn nữ:
\({\bar x_{nữ}} = \frac{{4.5 \times 4 + 5.5 \times 8 + 6.5 \times 10 + \times 7.5 \times 11 + 8.5 \times 8}}{{4 + 8 + 10 + 11 + 8}} = 6.77\).
6.77 > 6.52. Như vậy thời gian ngủ trung bình của các bạn nữ nhiều hơn các bạn nam.
b) Cỡ mẫu n = 86.
Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_{21}} + {x_{22}}}}{2}\). Do \({x_{21}},\;{x_{22}}\) đều thuộc nhóm \(\left[ {5;6} \right)\) nên nhóm này chứa \({Q_1}\). Do đó, \(p = 2;\;\;{a_2} = 5;\;\;{m_4} = 18;\;\;{m_1} = 10;\;{a_3} - {a_2} = 6 - 5 = 1\).
Ta có: \({Q_1} = 5 + \frac{{\frac{{86}}{4} - 10}}{{18}} \times 1 = 5,63(8)\).
Ý nghĩa: Có 75% học sinh khối 1 ngủ ít nhất 5,63(8) giờ.
Bài 3.7 trang 67 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của một đại lượng. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức về đạo hàm, bao gồm đạo hàm của hàm số tại một điểm, đạo hàm của các hàm số cơ bản, và các quy tắc tính đạo hàm.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Thông thường, bài tập này sẽ yêu cầu tính đạo hàm của một hàm số tại một điểm cụ thể, hoặc tìm điều kiện để hàm số có đạo hàm tại một điểm. Ngoài ra, đề bài có thể yêu cầu sử dụng đạo hàm để giải quyết các bài toán liên quan đến tối ưu hóa, chẳng hạn như tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của một hàm số.
Giả sử đề bài yêu cầu tính đạo hàm của hàm số f(x) = x2 + 2x + 1 tại điểm x = 0. Ta thực hiện các bước sau:
Khi giải bài tập này, học sinh cần lưu ý một số điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Để học tập và ôn luyện kiến thức về đạo hàm và giải Bài 3.7 trang 67 SGK Toán 11 tập 1 một cách hiệu quả, học sinh có thể tham khảo các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, học sinh có thể tự tin giải quyết Bài 3.7 trang 67 SGK Toán 11 tập 1 - Kết nối tri thức và nắm vững kiến thức về đạo hàm.