Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2 - Kết nối tri thức. Mục 2 trang 78 là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Để nghiên cứu mối liên quan giữa thói quen hút thuốc lá với bệnh viêm phổi, nhà nghiên cứu chọn một nhóm 5 000 người đàn ông.
Đề bài
Để nghiên cứu mối liên quan giữa thói quen hút thuốc lá với bệnh viêm phổi, nhà nghiên cứu chọn một nhóm 5 000 người đàn ông. Với mỗi người trong nhóm, nhà nghiên cứu kiểm tra xem họ có nghiện thuốc lá và có bị viêm phổi hay không. Kết quả được thống kê trong bảng sau:
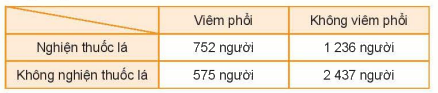
Từ bảng thống kê trên, hãy chứng tỏ rằng việc nghiện thuốc lá và mắc bệnh viêm phổi có liên quan với nhau.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Với hai biến cố A và B, nếu \(P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\) thì A và B không độc lập.
Lời giải chi tiết
Chọn ngẫu nhiên một người đàn ông
Gọi A là biến cố “Người đó nghiện thuốc lá”, B là biến cố “Người đó mắc bệnh viêm phổi”
Khi đó, AB là biến cố “Người đó nghiện thuốc lá và mắc bệnh viêm phổi”
Ta có \(P\left( A \right) = \frac{{752 + 1236}}{{5000}} = \frac{{497}}{{1250}};P\left( B \right) = \frac{{752 + 575}}{{5000}} = \frac{{1327}}{{5000}}\)
\( \Rightarrow P\left( A \right).P\left( B \right) = \frac{{497}}{{1250}}.\frac{{1327}}{{5000}} = 0,10552304\)
Mặt khác \(P\left( {AB} \right) = \frac{{752}}{{5000}} = 0,1504\)
Vì \(P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\) nên hai biến cố A và B không độc lập.
Vậy việc nghiện thuốc lá và mắc bệnh viêm phổi có liên quan với nhau.
Mục 2 trang 78 SGK Toán 11 tập 2 - Kết nối tri thức thường tập trung vào các bài toán liên quan đến đạo hàm của hàm số. Cụ thể, các bài tập thường yêu cầu học sinh tính đạo hàm của các hàm số đơn giản, áp dụng quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp. Việc nắm vững các quy tắc này là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Để giúp các em học sinh giải quyết các bài tập trong mục 2 trang 78 một cách hiệu quả, chúng tôi sẽ trình bày chi tiết lời giải của từng bài tập. Dưới đây là một ví dụ minh họa:
Lời giải:
Trong mục 2 trang 78, các bài tập thường được chia thành các dạng sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 78 SGK Toán 11 tập 2 - Kết nối tri thức. Hãy luyện tập thường xuyên và áp dụng các kiến thức đã học vào giải các bài tập tương tự để nâng cao kỹ năng giải toán của mình. Chúc các em học tập tốt!